Perímetro, área e volume são cálculos que equivalem às medidas das figuras geométricas. Esse estudo matemático, que pertence à Geometria, lida com os desenhos conhecidos do nosso cotidiano, como triângulos, quadrados, círculos e todas as formas que englobam as figuras geométricas.
É por meio dessa matéria que conseguimos projetar e visualizar os formatos e espaços geométricos que essas figuras ocupam, bem como entender suas propriedades e realizar os cálculos necessários para dimensioná-los.
Os tipos de geometria variam conforme o número de dimensões da figura. Aquelas que tem duas dimensões (altura e largura), como uma folha de papel, são estudadas pela Geometria Plana e chamadas de “figuras planas”, porque podem facilmente ser representadas no plano cartesiano.
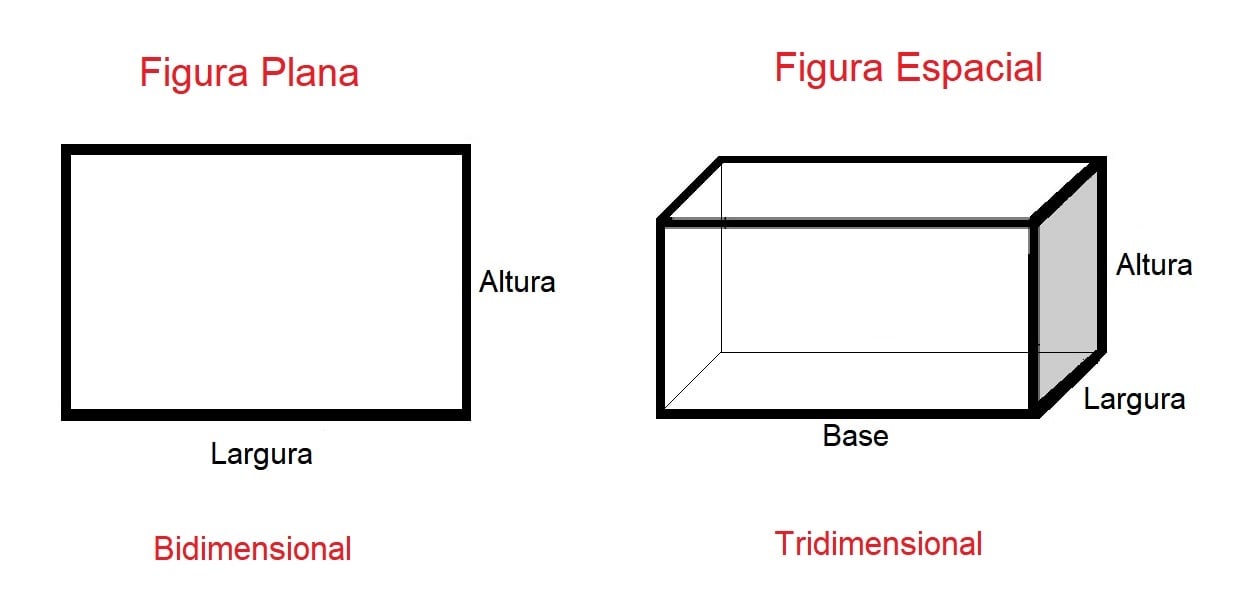
Já as figuras que possuem três dimensões (altura, largura e profundidade) são estudadas pela Geometria Espacial, porque são representadas por um plano mais palpável. Como exemplo podemos citar os objetos sólidos que encontramos ao nosso redor no dia-a-dia, como uma caixa de papelão ou uma bola de futebol.
Diante disso, podemos resumir que a área mede a superfície de uma figura plana, o perímetro mede o comprimento do seu contorno e o volume calcula o espaço ocupado pela figura tridimensional.
Para entender melhor cada um desses conceitos e como realizar o cálculo dessas medidas vamos aprofundar o nosso estudo.
O que é perímetro?
O perímetro mede o comprimento do contorno das figuras, — sejam elas planas, espaciais ou até mesmo não geométricas — por meio do somatório das medidas do seu contorno.
Imagine um barbante contornando uma folha de papel. Agora estique o barbante e meça o seu tamanho com uma régua. O resultado equivale ao valor do perímetro!
Para explicar esse conceito sobre as figuras geométricas, vamos utilizar o recurso do desenho para visualizar melhor as suas delimitações. Observe:
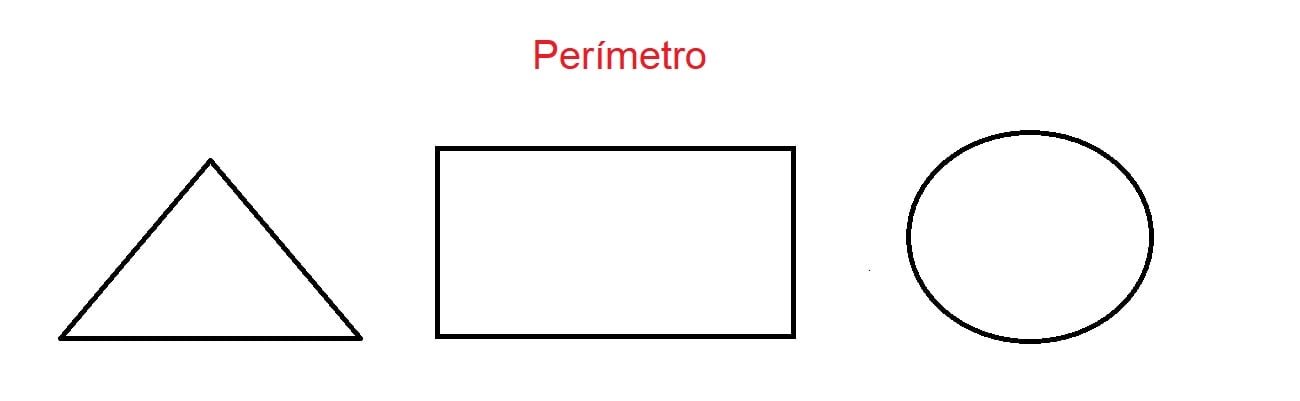
Nas imagens acima, podemos identificar que a linha preta é o contorno que delimita e cria as figuras dos desenhos, dando a sua forma de triângulo, retângulo e círculo, respectivamente.
Cada uma das arestas conectadas pelas intersecções compõe um dos lados da figura. O perímetro, por sua vez, calcula a soma das medidas do contorno do desenho, ou seja, o comprimento da figura.
Digamos que você queira comprar uma moldura para um quadro, por exemplo. Para saber o tamanho exato do encaixe do objeto, devemos conhecer as medidas de cada um dos seus lados.
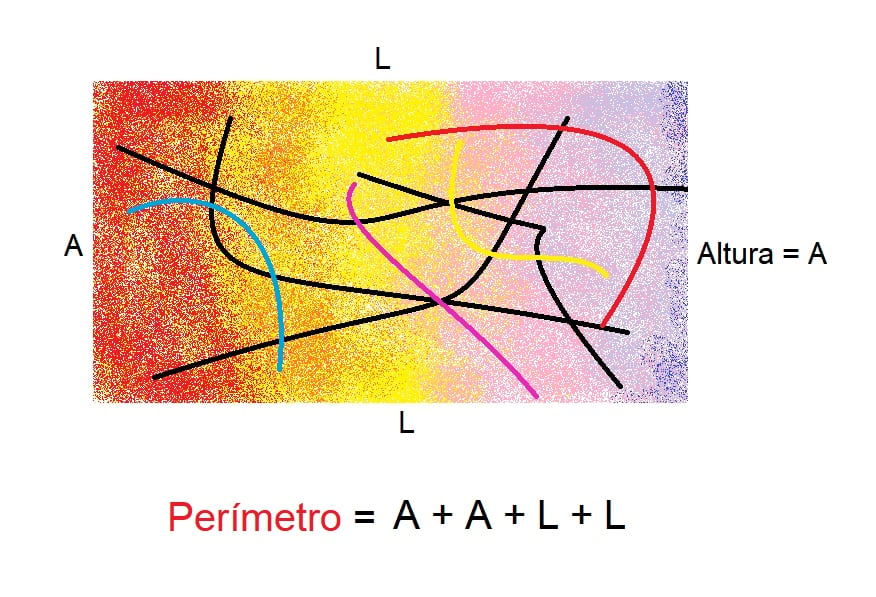
Se o quadro tiver o formato de um retângulo, a moldura precisará acompanhar o mesmo desenho. Digamos, então, que o quadro possui 1 metro de largura por 2 metros de altura.
Para descobrir o comprimento da moldura precisaremos somar os dois lados da altura e os dois lados da largura.
Assim, teremos: 1 + 2 + 1 + 2, que dá a volta completa no objeto. O resultado do perímetro da moldura será, portanto, de 6 metros.
Como calcular o Perímetro?
Como dissemos anteriormente, o perímetro se refere à medida de um comprimento de um contorno. Para calculá-lo, devemos somar as medidas de todos os lados da figura.
Imagine um jogador de futebol. Durante o seu treino ele dá duas voltas completas ao redor do campo. Para calcular quantos metros o jogador irá correr, devemos calcular o comprimento do espaço. Veja:
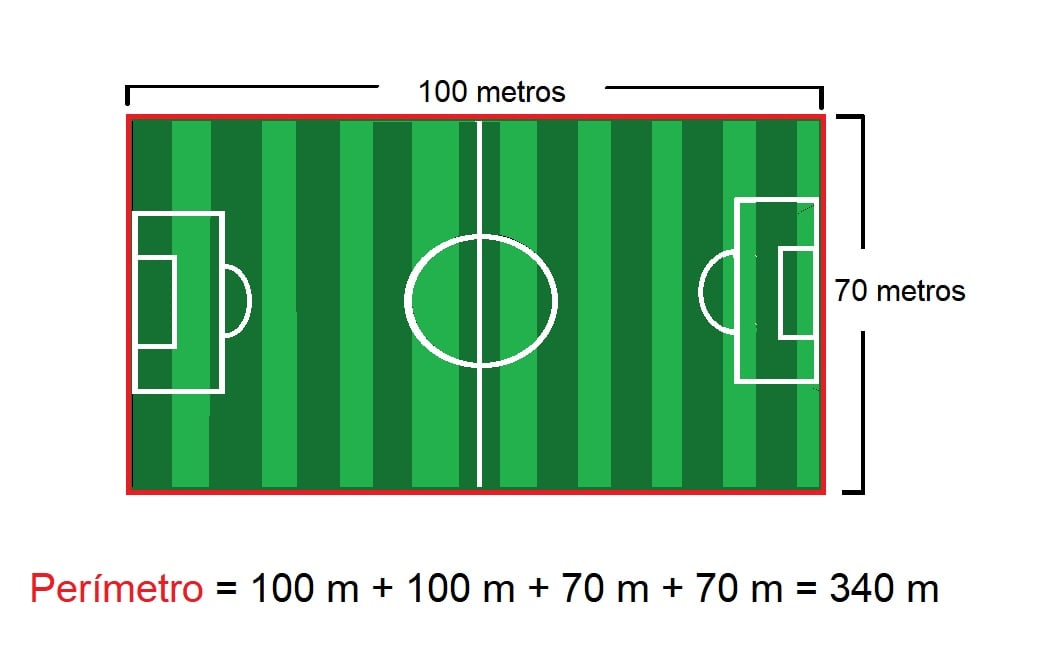
Se o perímetro do campo de futebol tem 340 metros, devemos calcular o dobro desse valor para identificar o total percorrido pelo jogador. Assim, 340 + 340 = 680 metros.
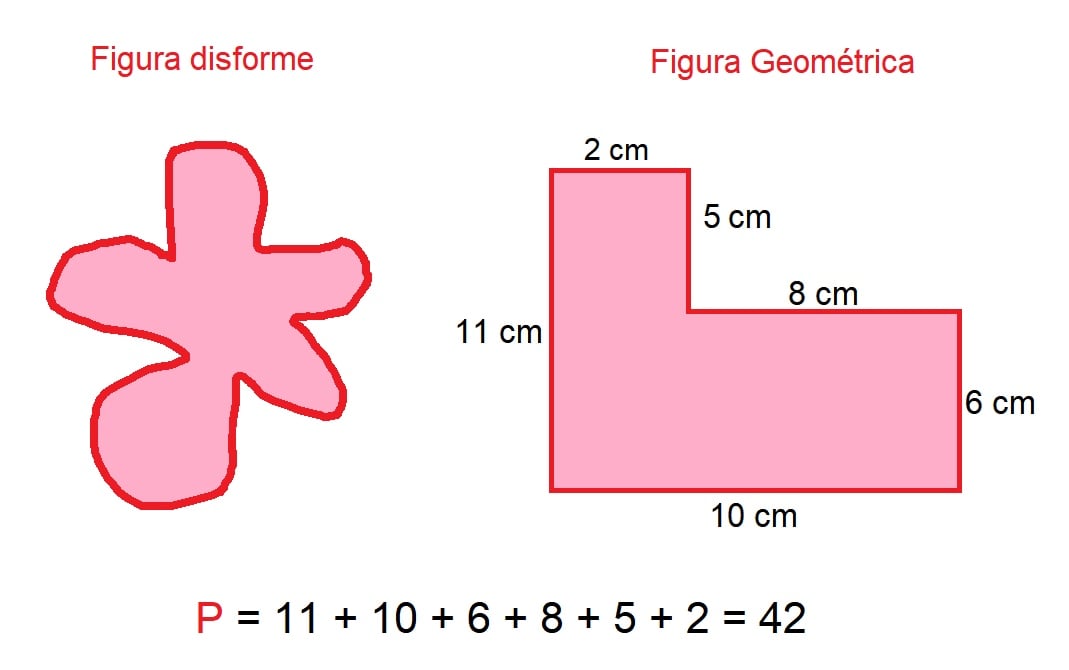
Pode ocorrer, entretanto, de um problema sugerir um desenho disforme, que não possibilita o cálculo de seu perímetro.
Para tornar o cálculo possível, devemos imaginar que contornamos a figura com um barbante e esticá-lo ao máximo, até que ele tome a forma de uma figura geométrica possível de ser calculada.
O perímetro de uma circunferência, por outro lado, exige outro tipo de cálculo. É importante primeiro saber que uma circunferência representa um lugar geométrico onde todos os pontos estão a mesma distância de um centro.
O raio de uma circunferência mede a distância do centro a um ponto qualquer do seu contorno e seu diâmetro é formado por dois raios que passam pelo seu centro.
O perímetro corresponde ao comprimento da circunferência. Se esticarmos o contorno da circunferência como uma reta iremos perceber que ela representa a medida de seu comprimento.
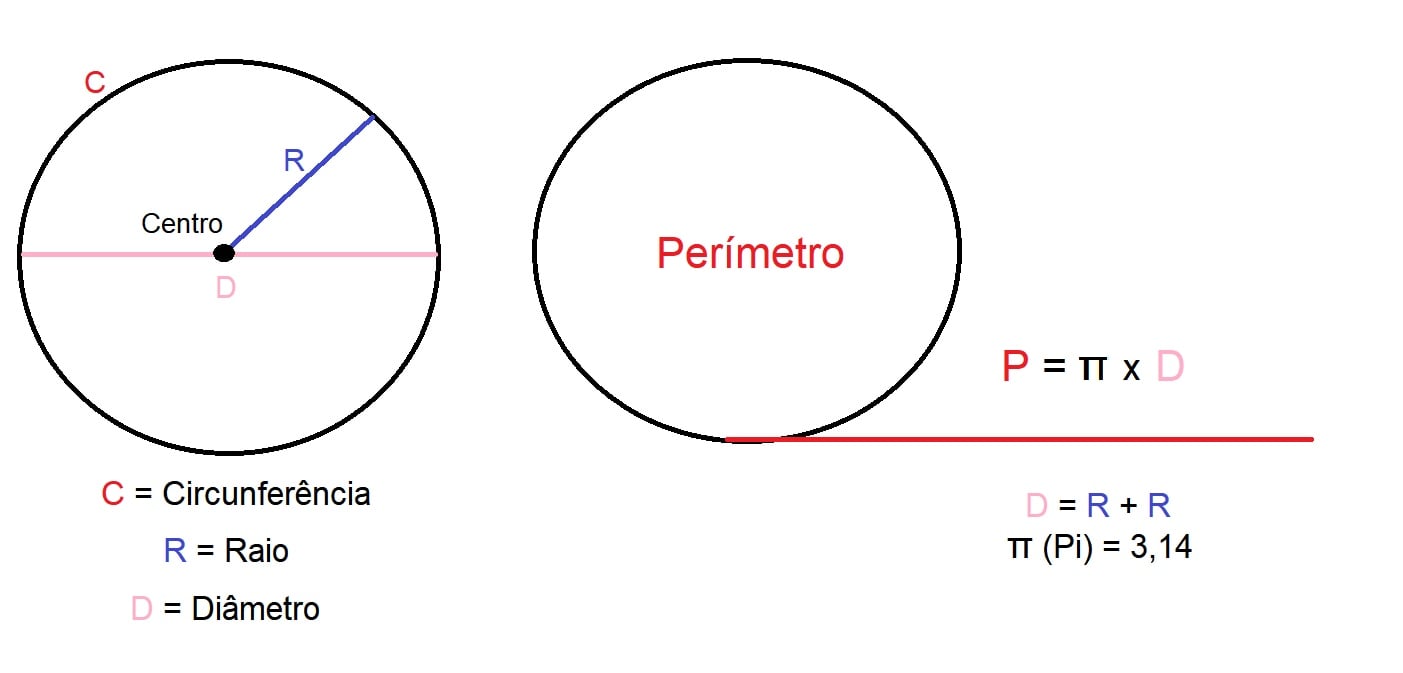
Para calcular o perímetro da figura utilizamos a fórmula: P = π (Pi) x D. Onde D é a medida do diâmetro do círculo e corresponde a soma de dois raios da circunferência.
Para conhecimento, o Pi é uma letra grega de 3 mil anos que representa uma constante matemática. O seu valor infinito de 3,14159… é costumeiramente simplificado apenas por 3,14.
Perímetro dos Objetos Espaciais
Por fim, há ainda os perímetros dos objetos tridimensionais. Nessas situações, devem ser somadas, da mesma maneira, todas as arestas que compõe o objeto.
No caso de um cubo, por exemplo, formado por 12 retas, devemos somar os valores de todos os lados ou multiplicar o valor de um lado por 12, uma vez que as medidas dos seus lados são iguais.
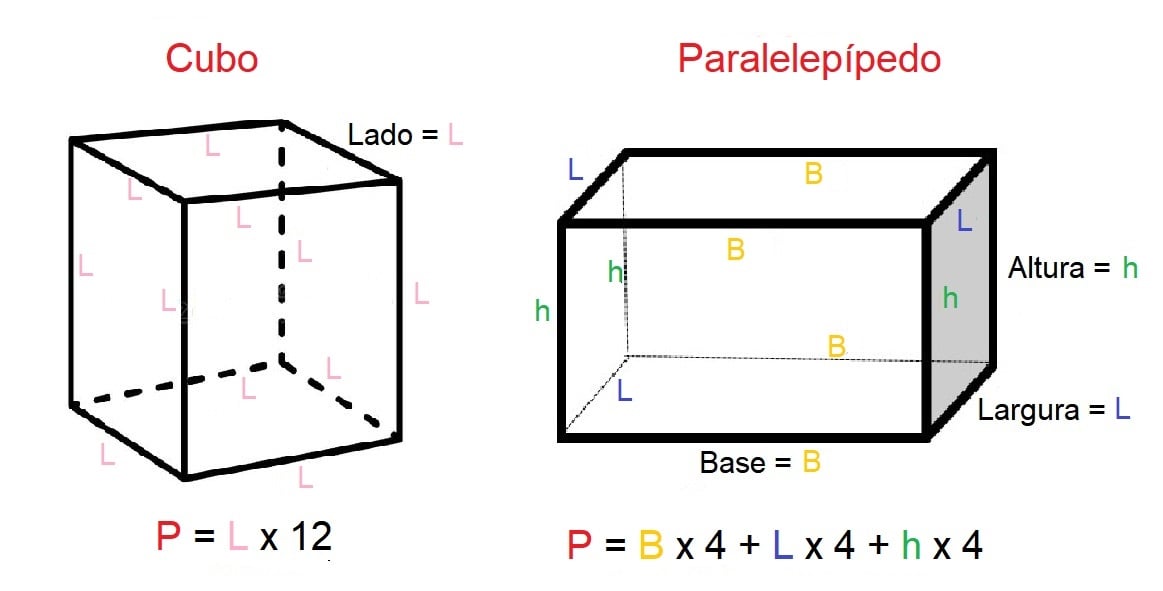
Na imagem acima, também podemos ver como exemplo o cálculo do perímetro de uma caixa retangular, chamada de paralelepípedo. Como seus lados não são idênticos, como no cubo, devemos somar (ou multiplicar) separadamente o valor dos contornos da base, largura e altura.
Considerando que A = 5 cm, L = 4 cm e B = 6 cm, podemos calcular que o perímetro é:
P = 5 + 5 + + 5 + 5 + 4 + 4 + 4 + 4 + 6 + 6 + 6 + 6 =
P = 5 x 4 + 4 x 4 + 6 x 4 =
P = 60 centímetros.
Unidades de medida do Perímetro
As unidades de medida utilizadas para se referir ao perímetro são iguais às unidades descritas pelo Sistema Métrico Decimal, sendo o metro a unidade principal, intermediado por seus múltiplos e submúltiplos.
- km = quilômetro;
- hm = hectômetro;
- dam = decâmetro;
- m = metro;
- dm = decímetro;
- cm = centímetro;
- mm = milímetro;
Se por acaso um problema apresentar unidades diferentes de medida será necessário primeiro uniformizar o sistema de medidas. Tomemos como exemplo um triângulo, com lados em centímetros, e a base em milímetros.
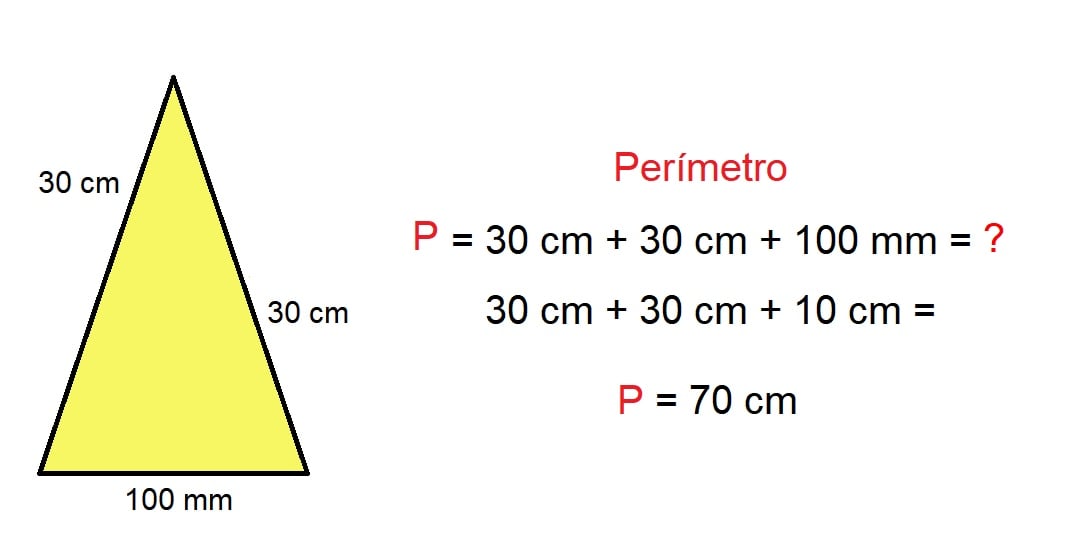
Optando pela unidade dos centímetros devemos transformar inicialmente a medida da base dada em milímetros. Sabendo que 1 cm corresponde a 10 mm, podemos concluir que 100 milímetros equivale igualmente a 10 centímetros.
Com todas as medidas seguindo a mesma unidade, agora o cálculo se torna possível. Sendo o perímetro o somatório de todos os lados do contorno do triângulo, devemos somar os dois lados mais o valor da base, o que dá o resultado de 70 centímetros.
Entretanto, é necessário verificar qual a medida exigida em uma questão. Se o problema pedir que a solução apresente a unidade de medida fundamental do metro, então será preciso converter todas as medidas conforme a exigência.
Nesta situação, cada lado do triângulo terá 0,3 metros e a base 0,1 metros. Assim: P = 0,3 + 0,3 + 0,1 = 0,7 metros.
O que é Área?
A área corresponde ao cálculo do espaço total de uma superfície, seja ela uma figura plana (bidimensional) ou sólida (tridimensional).
Para entendermos melhor essa definição, voltaremos ao mesmo desenho apresentado no início do estudo, agora totalmente preenchido por cores.
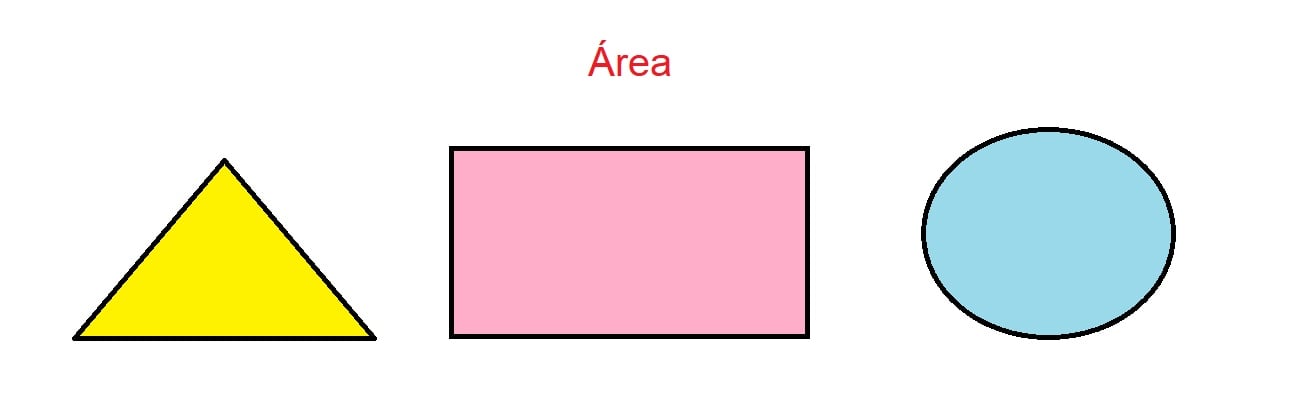
Nas imagens acima, observamos novamente que a linha preta é o perímetro, ou seja, o contorno que delimita as figuras. A área, por sua vez, é todo o preenchimento colorido que ocupa o espaço dentro do contorno.
Ou seja, a área mede a superfície de uma figura (base x altura), sendo que cada forma geométrica possui uma fórmula específica para calcular sua área.
Imagine que você queira pintar uma parede toda de azul, por exemplo. Para saber quantos litros de tinta serão necessários para preencher todos os espaços será necessário calcular a medida da área da folha.
Ou por outra, podemos usar o exemplo da construção civil. Quando vamos comprar o piso para a casa precisamos ter conhecimento do cálculo da área para saber quanto material será necessário para cobrir completamente a região delimitada.
Da mesma forma, o preço dos imóveis é calculado de acordo com o valor do metro quadrado. Para saber o preço total de uma casa ou apartamento precisamos, então, conhecer a medida total da área do imóvel.
É importante ressaltar também que existe o cálculo dos objetos espaciais. Nesse caso, as fórmulas matemáticas são mais complexas e devemos levar em conta toda a “casca” que envolve o objeto sólido.
Imagine por exemplo um cubo feito a partir de um pedaço de papel. Nessa situação, a figura plana foi transformada em um objeto sólido, palpável, que possui várias faces, inclusive volume, porque há um espaço oco dentro desse objeto, preenchido por ar.
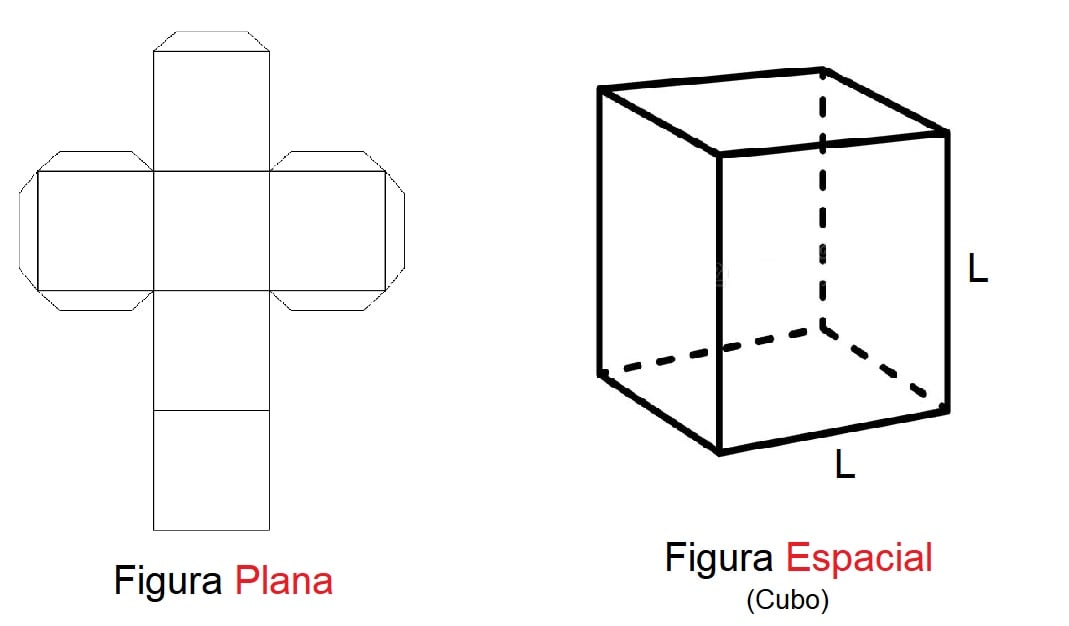
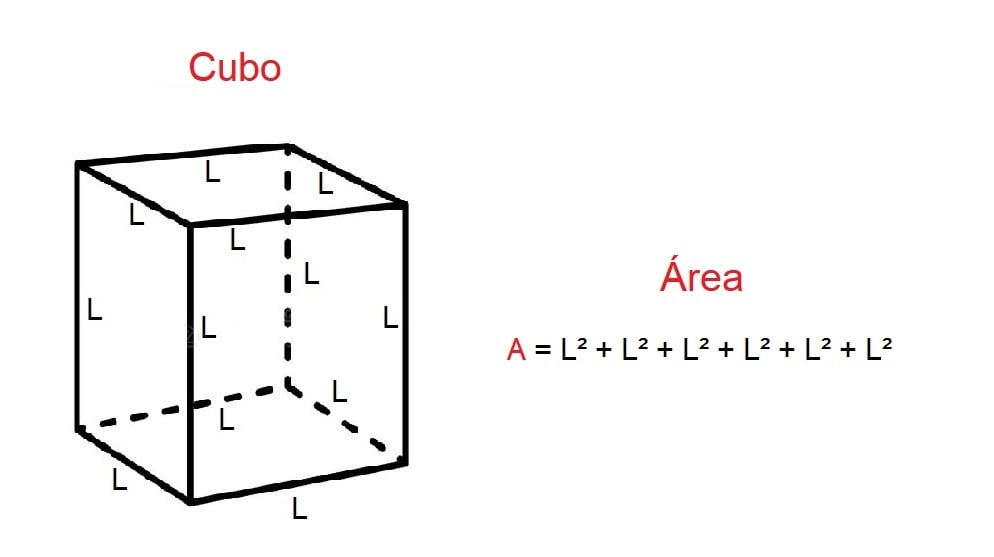
Para calcular a área total de um objeto sólido, devemos então somar o valor das áreas de cada face do objeto. No caso do cubo, que possui seis lados formados por quadrados idênticos, devemos antes de tudo, aprender a calcular a área da figura plana do quadrado. Acompanhe:
Como calcular a área?
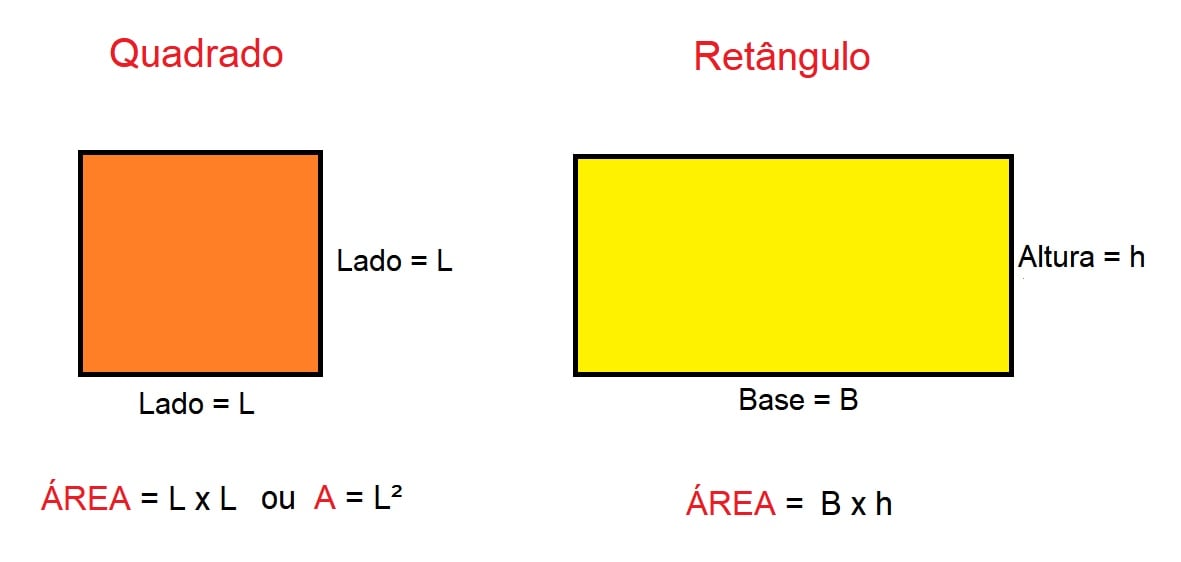
Reforçamos que cada figura geométrica tem o seu próprio modo de calcular a área. Assim, para descobrir a área de um quadrado devemos multiplicar o lado vezes o lado, uma vez que todos os lados da figura possuem a mesma medida.
Portanto: A = L x L = L²
Já para descobrir a área de uma região retangular devemos multiplicar a medida da base pela medida da altura. Assim: A = B x h
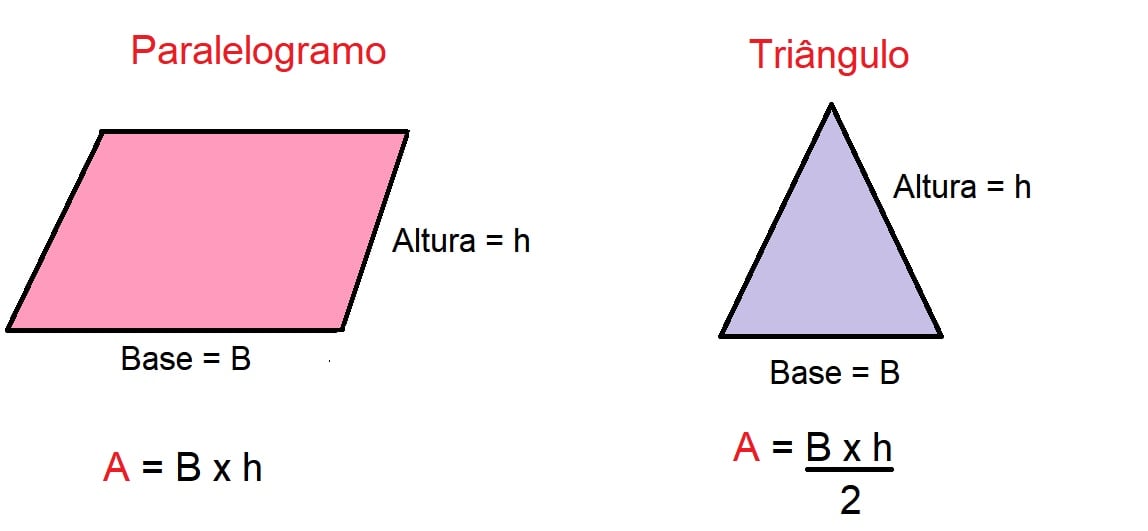
No caso de uma região limitada por um paralelogramo devemos multiplicar a medida da base vezes a medida da altura do desenho.
Já a área de um triângulo qualquer é calculado pela medida da base vezes a medida da altura, dividido por 2.
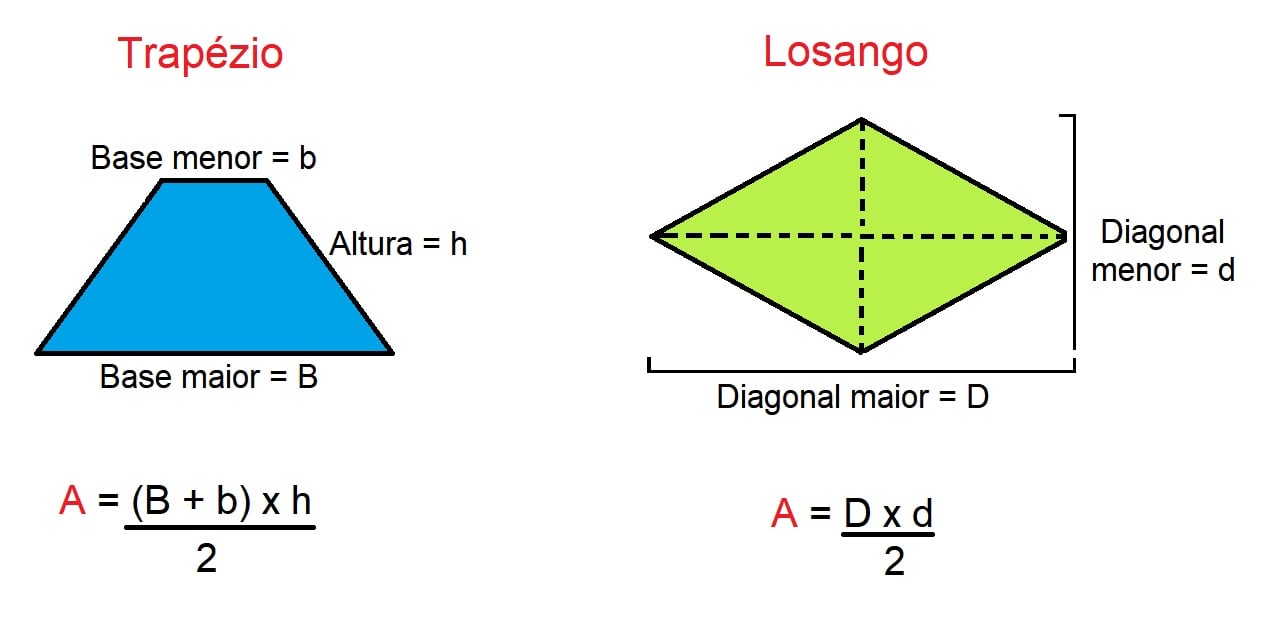
A área de uma região limitada por um trapézio, por sua vez, exige a medida da “base maior” mais a medida da “base menor” multiplicado pela “altura”, dividido por 2.
Enquanto a área de uma figura de um losango é calculada pela medida da “diagonal maior” vezes a medida da “diagonal menor”, dividido por 2.
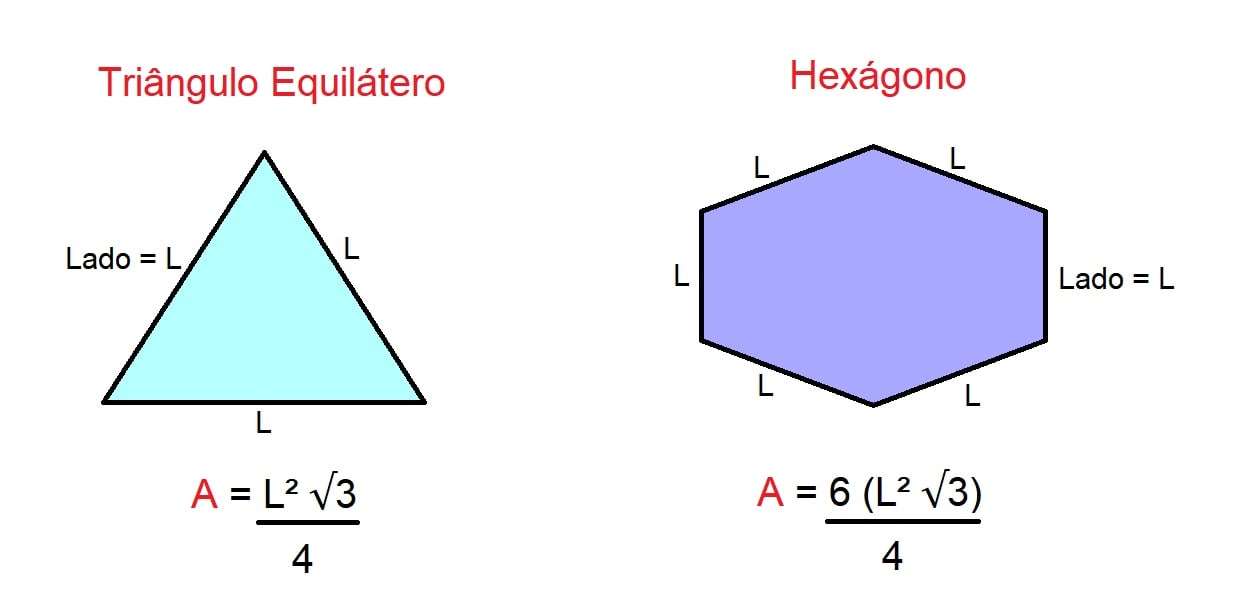
No caso do triângulo equilátero, que possui todos os lados iguais, a área é medida pelo lado elevado ao quadrado, vezes a raiz quadrada de 3, dividido por 4.
Já para descobrir a área do hexágono devemos multiplicar primeiro o conteúdo dentro do parêntesis. Assim, o lado elevado ao quadrado, vezes a raiz quadrada de 3, vezes 6, dividido por 4.
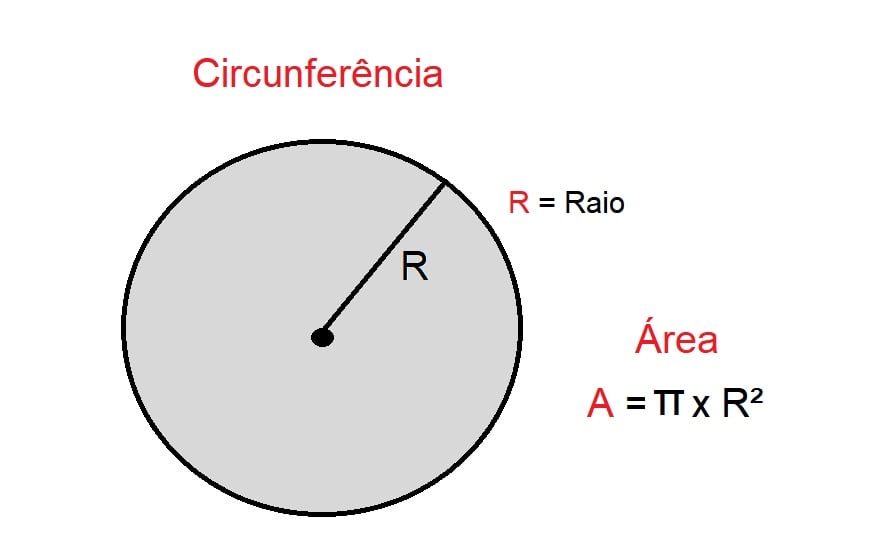
Por fim, a área de um círculo é calculada pelo valor de π (Pi) vezes a medida do Raio da Circunferência elevado ao quadrado.
Se considerarmos que o valor do raio é igual a 2 m, por exemplo, então o resultado da área da circunferência será de:
A = π x R²
A = 3,14 x 2²
A = 12,56 m²
Todas as figuras apresentadas são estudadas pela Geometria Plana e tratam-se de figuras bidimensionais, ou seja, possuem apenas duas dimensões: altura e largura.
Área de figuras espaciais
No caso mais complexo das figuras espaciais, também chamadas de tridimensionais, calculamos primeiro as áreas de cada face, de acordo com o desenho e medidas que elas apresentam.
Utilizando novamente o exemplo do cubo, formado por 6 quadrados perfeitos, devemos primeiro calcular o valor da área de um dos lados e depois somar esse valor seis vezes ou multiplicar o resultado da área por 6. Veja:
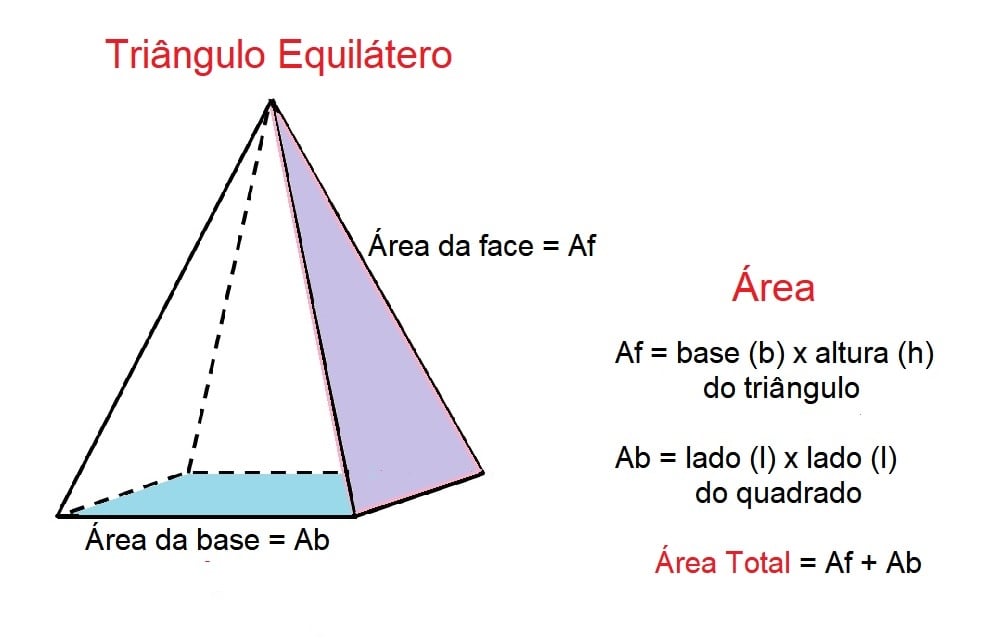
Se a figura, por outro lado, for uma pirâmide, — que pode ser equilátera ou não — ela será composta por faces e uma base que dá sustentação ao objeto sólido.
Para descobrir o valor de sua área, então, precisamos calcular o valor da área da base, depois o valor da área da face. O somatório dos dois valores dará o resultado da área total do objeto. Observe:
Unidades de medida da Área
Toda unidade de área é dada ao quadrado porque multiplicamos as medidas de duas dimensões. Logo, o valor da largura multiplicado pelo valor da altura resulta em uma área ao quadrado.
No caso da unidade fundamental, a medida seria representada pelo m², ou seja, metro ao quadrado.
No entanto, podemos identificar situações onde a unidade de medidas utilizadas serão os múltiplos e submúltiplos da unidade principal. Assim, podemos encontrar como exemplo:
- km²: quilômetro quadrado;
- hm²:hectômetro quadrado;
- dam²:decâmetro quadrado;
- m²:metro quadrado;
- dm²:decímetro quadrado;
- cm²:centímetro quadrado;
- mm²:milímetro quadrado.
Como o valor da área total deve ser representado por uma única medida, se o exemplo utilizar medidas diferentes, devemos primeiro transformar tudo para a unidade do metro.
Mas se uma questão de um vestibular, por exemplo, não especificar a medida a ser utilizada, você poderá escolher qual será a unidade em destaque.
Suponhamos que uma personagem chamada Ana deseja adquirir um tapete retangular que cubra a área total de sua sala. Após realizar as devidas medidas do espaço, Ana descobriu que seu ambiente possui 3 metros de largura e 547 centímetros de altura. Qual será a área total do tapete, em metros, para cobrir completamente a sala?
Para descobrir a solução do problema, devemos primeiro transformar a medida de centímetros para metro. Sabendo que a unidade dos centímetros corresponde a 100 vezes a unidade do metro, devemos caminhar duas casas com a vírgula, para a direita.
Assim: 547 cm = 5,47 m
Desta maneira, podemos concluir que a sala possui 5,47 metros de altura. Tendo convertido a medida, resta apenas multiplicar a largura vezes a altura da sala.
Área = largura x altura = 3 x 5,47 = 16,41 m².
Como Ana deseja cobrir todo o espaço, ela deverá encontrar um tapete que tenha exatamente a medida de 16, 41 metros quadrados, ou que se aproxime ao máximo da área total do ambiente.
É comum no início do estudo confundir os conceitos das medidas e seus cálculos. Por isso, é importante conhecer e reforçar primeiro o estudo de todas as medidas das figuras planas, para só então prosseguir os cálculos dos objetos tridimensionais.
O que é Volume?
Quando falamos da medida do volume estamos abordando, invariavelmente, as figuras tridimensionais. Isso porque o volume só pode estar presente em objetos sólidos, que possuem um espaço oco em seu interior que pode ser preenchido.
Como exemplo, podemos citar o cubo, o paralelepípedo, o cilindro, a pirâmide e os prismas, sendo que os prismas são objetos geométricos formados por segmentos de reta paralelos, cujas extremidades são polígonos também paralelos.
Assim, é correto dizer que as figuras planas não possuem volume e essa medida não pode ser calculada, ficando o cálculo restrito apenas aos corpos sólidos.
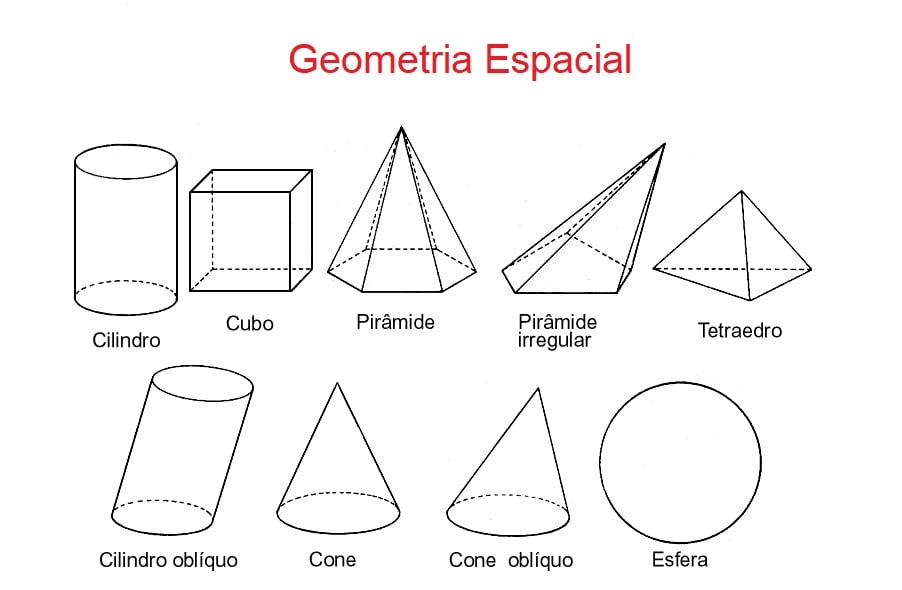
Podemos dizer que o volume de um corpo equivale a quantidade de espaço ocupada por este mesmo corpo. Em outras palavras, o volume se refere a quantidade de espaço que um objeto ocupa.
Para estacionarmos um carro, por exemplo, precisamos calcular (mesmo que intuitivamente), o volume de espaço que o automóvel ocupará dentro da vaga. Da mesma maneira, a água dentro de uma garrafa representa o volume que cabe dentro do utensílio.
Como calcular o Volume?
O cálculo do volume é sempre dado pela multiplicação da altura (h), vezes a largura (L), vezes o comprimento (C).
No entanto, alguns materiais sólidos como os cones, cilindros, pirâmides e esferas possuem fórmulas próprias, uma vez que suas dimensões e formas são específicas.
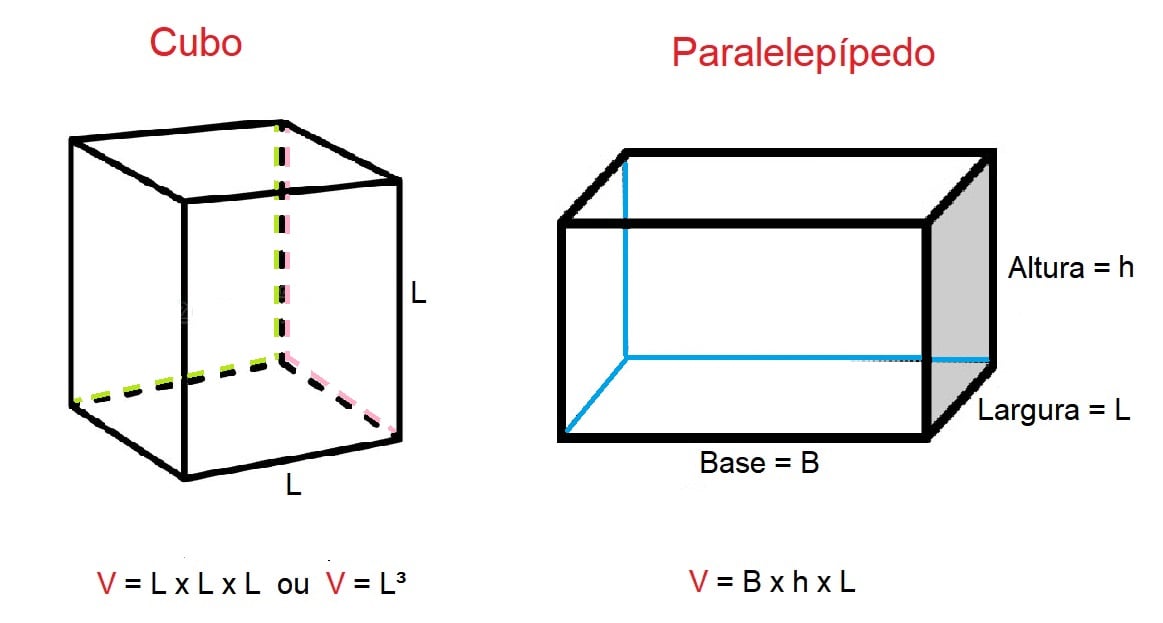
Para calcular o volume de um cubo, por exemplo, precisamos multiplicar por três a medida do lado, uma vez que a figura possui três dimensões.
Assim, V = L x L x L ou V = L³
Já o volume de um paralelepípedo é calculado pela medida do comprimento, vezes a medida da largura, vezes a medida da altura. Ou: V = B x L x h.
O volume de um prisma qualquer, por sua vez, é dado pelo produto da área vezes a altura.
Desta forma: V = A x h.
Sendo que A é igual o cálculo da área da base. Assim, devemos observar primeiro o formato da base que sustenta o objeto. Se a base for triangular (3 lados) deverá ser utilizado o cálculo da área do triângulo, para posteriormente multiplicar o resultado pela altura.
Da mesma maneira, para obter o volume de um prisma quadrangular (quatro lados), pentagonal (5 lados), hexagonal (6 lados) ou octogonal (oito lados) deve ser realizado o cálculo da área do pentágono, hexágono e octógono, respectivamente, para só então multiplicar o resultado pela altura do objeto.
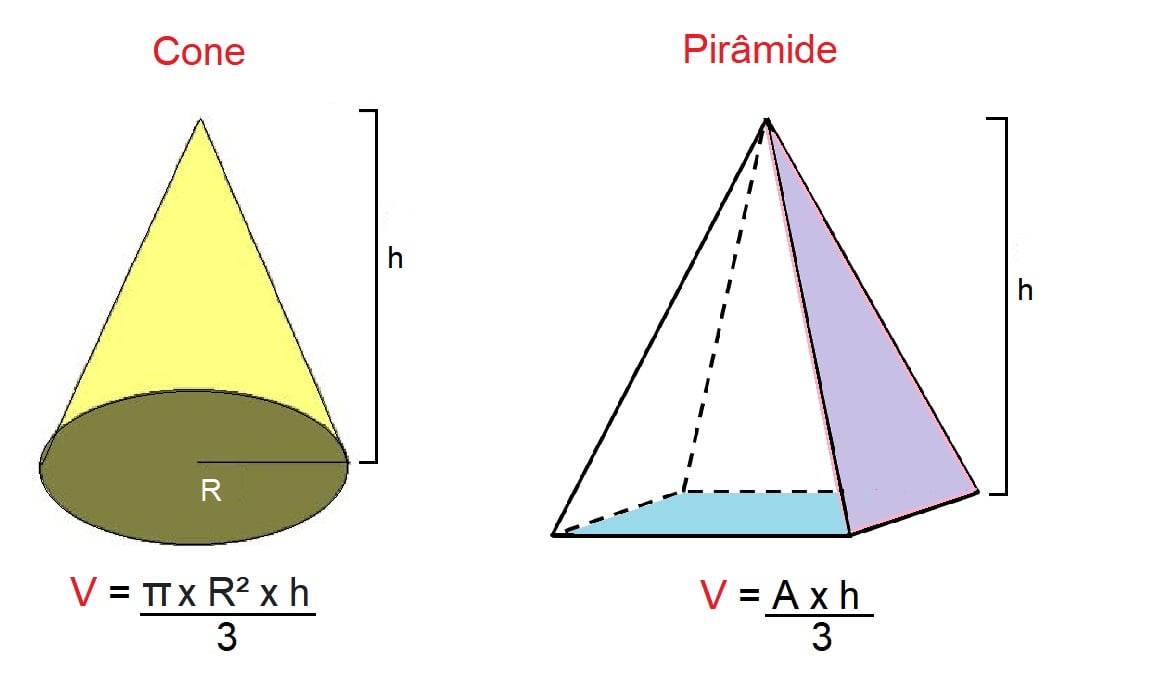
Para calcular o volume de um cone, por outro lado, devemos multiplicar π (Pi) pelo raio ao quadrado, vezes a altura, dividido por 3.
Enquanto no volume da pirâmide é calculado o valor da área da base, vezes a altura, dividido por 3. Sendo que a cálculo da área da base depende do formato da figura.
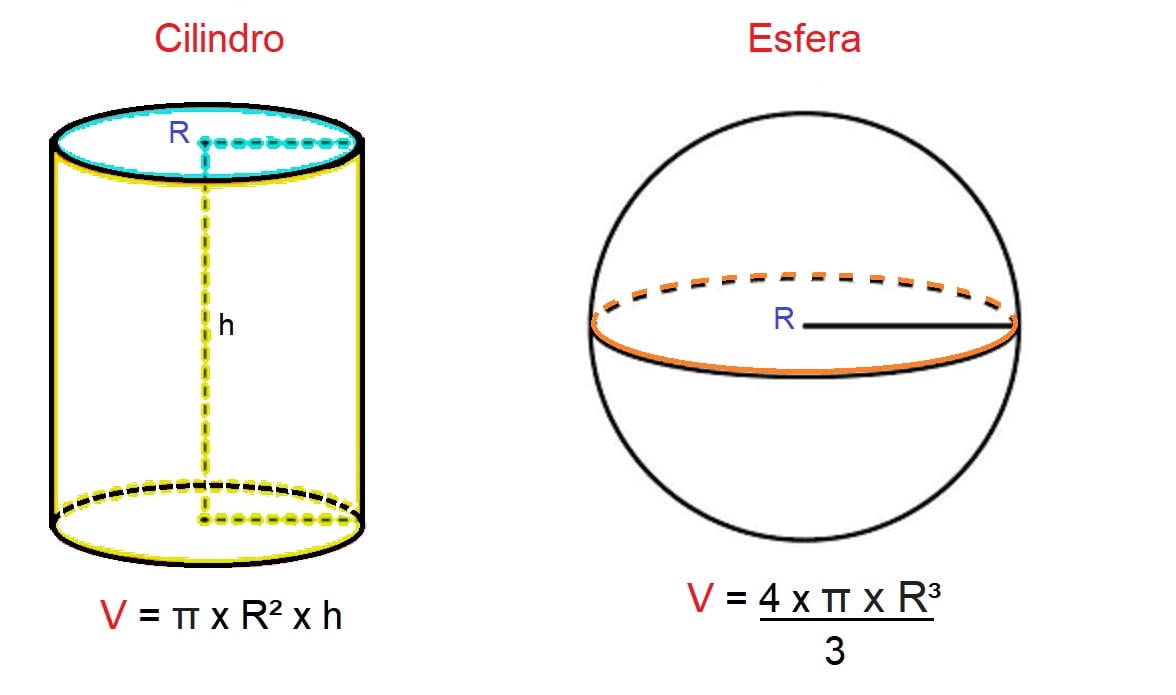
O volume do cilindro, por outro lado, se dá pelo cálculo de π (Pi), vezes o raio ao quadrado, vezes a altura.
Por fim, para obter o resultado do volume de uma esfera devemos multiplicar 4 vezes π (Pi), vezes o raio ao cubo, dividido por 3.
Suponhamos que o raio da esfera meça 3 cm. Qual será o valor do volume?
Para tanto, V= 4 x π x R³ = V= 4 x 3,14 x 3³ = V= 113, 04 cm³
_______________ _______________
3 3
Unidades de medida do Volume
Toda unidade de volume é representada ao cubo, uma vez que consideramos as três dimensões da figura espacial. Considerando que a medida fundamental do volume é o metro cúbico (m³), seus múltiplos e submúltiplos são:
- km³ = quilômetro cúbico;
- hm³ = hectômetro cúbico;
- dam³ = decâmetro cúbico;
- m³ = metro cúbico;
- dm³ = decímetro cúbicos;
- cm³ = centímetro cúbico;
- mm³ = milímetro cúbico.
Para executar a conversão da unidade principal para suas unidades múltiplas basta multiplicar o valor por mil. Quanto aos submúltiplos, basta dividir a medida por 1000.
No entanto, é importante considerarmos que o volume é, geralmente, representado pela medida do litro no nosso dia-a-dia. Assim, também devemos considerar as seguintes unidades de medida:
- kl: kilolitro;
- hl: hectolitro;
- dal: decalitro;
- L: litro;
- dl: decilitro;
- cl: centilitro;
- ml: mililitro.
Para resolver questões que utilizam a unidade do metro, por exemplo, mas que pede a solução do problema em litros, é necessário considerar que 1 dm³ é igual a 1 litro.
Diferenças entre Perímetro, Área e Volume
Para reforçar o estudo vamos destacar finalmente a diferença entre as medidas que dimensionam as figuras e objetos sólidos na Geometria. Devemos ressaltar que enquanto o perímetro e a área estudam tanto o universo dos desenhos planos quanto espaciais, o volume se restringe apenas à análise dos objetos sólidos, espaciais.
Apesar do conceito geral do perímetro dizer que seu cálculo é dado pela “soma de todos os lados”, devemos considerar que algumas figuras, como o cilindro, por exemplo, não possui lados. Assim, é importante ter a noção de que nesses casos, o perímetro será a soma do contorno da figura, sendo ela geométrica ou não.
O conceito da área pode ser complicado para ser absorvido, uma vez que seus cálculos não possuem um padrão e diversas formas geométricas possuem suas fórmulas específicas. Portanto, é necessário ter em mente que a área representa a delimitação interna de um polígono.
Já o volume é conhecido por ser o preenchimento que ocupa o espaço de um polígono ou uma forma geométrica. Desta maneira, para realizar o cálculo do volume é preciso considerar as três dimensões do objeto.
Assim, o perímetro é a soma dos segmentos de retas que formam a figura, chamados de lados (l). A área de uma figura é obtida pela multiplicação da base (b) pela altura (h). E o volume é determinado pela multiplicação da altura pela largura e pelo comprimento.
Diante disso, podemos resumir que a área mede a superfície de uma figura plana, o perímetro mede o comprimento do seu contorno e o volume calcula o espaço ocupado pela figura tridimensional.








