Quando o assunto é matemática básica, um conteúdo muito importante são os números primos, por isso é fundamental conhecer a definição dessa classe numérica e, claro, aprender a identificar quais são esses números.
O que é um número primo?
Números primos são os números naturais, ou seja, números inteiros não negativos, que são divisíveis somente por dois divisores: o número 1 e ele mesmo.
Estudados há mais de um milênio, os números primos intrigam matemáticos, cientistas e curiosos que até hoje esperam encontrar uma fórmula perfeita para descobrir números primos formados por sequências longas, com muitos dígitos.
Como saber se um número é primo ou não?
Partindo da definição de número primo, é fácil perceber que o número 3, por exemplo, pertence a essa categoria, uma vez que pode ser dividido por 1 e por ele mesmo, ou seja, 3, de modo que o resultado seja um número inteiro: 3/1 = 3 e 3/3 = 1.
Nem sempre, no entanto, é possível saber tão facilmente se um número é primo ou não, especialmente quando falamos de números grandes. A primeira coisa a ter em mente em relação à classificação de números primos é o conceito de divisor.
Nas frações em que o resultado é um número exato, ou seja, sem decimais, esse número é chamado de divisor. A identificação de um número primo depende de seus divisores e, quando um número apresenta apenas dois divisores (1 e ele mesmo), temos um número primo.
O número 16, por exemplo, não é primo, afinal ele pode resultar em mais de dois números exatos, e os números que o dividem são:
- D(16) = 1, 2, 4, 8 e 16.
Agora, se pensarmos no número 13, percebemos que ele tem apenas dois divisores, o que o classifica como um número primo:
- D(13) = 1 e 13.
Existe um método que ajuda a identificar números primos, chamado de Crivo de Eratóstenes. Com ele, é possível eliminar alternativas de uma forma bem prática. No exemplo abaixo, listamos todos os números de 1 a 100:
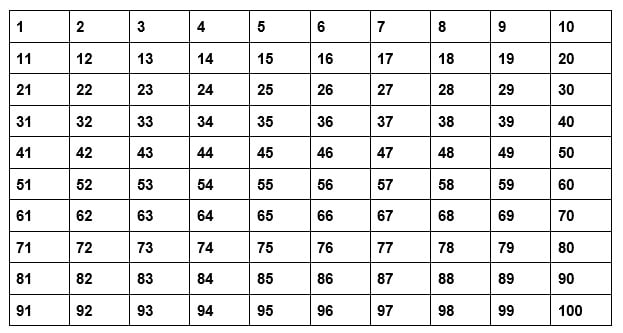
O número 1 tem somente um divisor, portanto ele não é um número primo. Já o número 2, que pode ser dividido por 1 e por ele mesmo, é um número primo, uma vez que tem somente dois divisores.
A partir do número 2, os outros números pares não são primos, já que todos podem ser divididos por 2. Abaixo, temos uma tabela que descarta todos os números que não são primos (em vermelho):
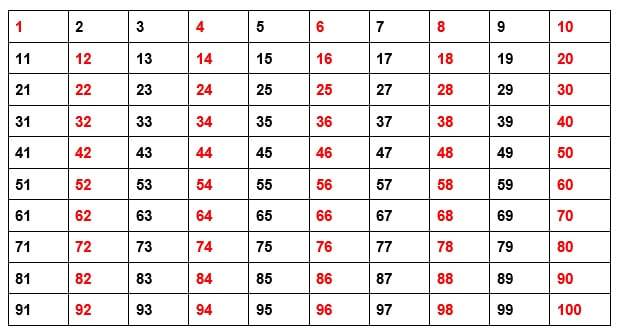
Agora, observando os números que restaram, percebemos que o 3 também é um número primo, já que só pode ser dividido por 1 e por ele mesmo. Seguindo essa lógica, podemos concluir que os números múltiplos de 3 não são números primos, o que nos permite descartar mais alguns números da lista (em azul):
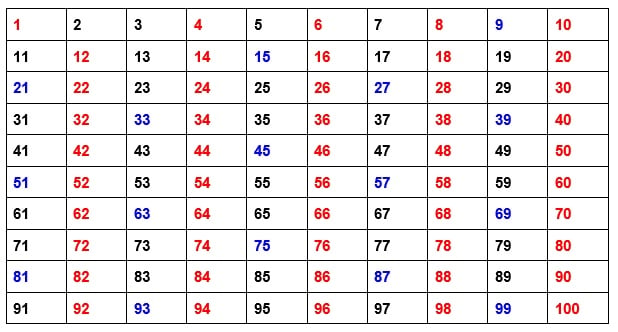
O número 5 também é primo, mas seus múltiplos, que são os números terminados em 5 ou 0, não são considerados primos. Marcamos estes números também (em verde; os números terminados em 0 já foram marcados em vermelho com base na lógica anterior):
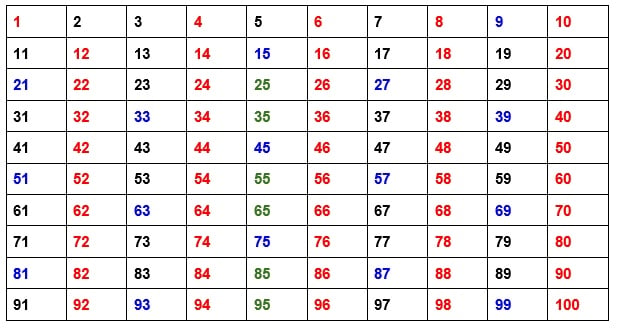
O número 7 também é primo, e é preciso desconsiderar também seus múltiplos, que ainda não foram destacados nas tabelas anteriores: 49, 77 e 91.
O crivo da tabela de 1 a 100 é concluído com o número 11, que é primo e não possui um divisores exatos além de 1 e 11. Seguindo esse raciocínio, vemos que os números restantes, que são os não foram coloridos, são os números primos de 1 até 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.
A tabela do Crivo de Eratóstenes pode servir também para números superiores a 100, como de 1 a 200 ou 1 a 500. Nesses casos, o processo de eliminação dos números que têm mais de dois divisores deve seguir até que se chegue ao resultado desejado.
Relação de números primos
Entre o número 1 e o número 1000, existem 168 números primos:
2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 |
47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 |
109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 | 179 | 181 |
191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 |
269 | 271 | 277 | 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 | 421 | 431 | 433 |
439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 |
523 | 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 | 607 | 613 |
617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 |
811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 | 887 |
907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Fatoração
Fatoração nada mais é do que a decomposição de qualquer número, primo ou não, em fatores primos. A decomposição é feita sucessivamente até que o resultado seja 1 – esse método é útil para o cálculo de mínimo múltiplo comum (MMC) e máximo divisor comum (MDC). Veja:
72/2 = 36
36/2 = 18
18/2 = 9
9/3 = 3
3/3 = 1
Repare que o número 2 aparece três vezes na fatoração, e o número 3 surge duas vezes, portanto, a decomposição de 72 em fatores primos equivale a 2³ x 3²; ou seja: 8 x 9 = 72.
Curiosidades sobre números primos
- Os números primos são o maior e mais antigo grupo numérico das ciências matemáticas, e o responsável por provar a infinidade dos números primos foi Euclides.
- Erastótones foi o primeiro matemático a encontrar um método simplificado para identificar os números primos. Esse método é chamado de Crivo de Erastótenes, como foi explicado anteriormente.
- A palavra “primo” tem relação com o termo “primeiro”, usado na escola pitagórica para organizar os números que não podem ser obtidos pela multiplicação de outros números naturais.
- Os números primos são utilizados para a criptografia de segurança para o compartilhamento de dados. O método RSA usa números primos para manter a segurança de todo e qualquer sistema financeiro virtual.
- O único número primo par é o 2.
- O número 1 não é considerado primo por ter apenas um divisor.
- O maior número primo já catalogado tem 24.862.048 dígitos, e foi encontrado por Patrick Laroche de Ocala, em 2018, na Flórida, nos EUA.
- O peruano Harald Andrés Helfgott descobriu, em 2013, a solução para um problema envolvendo números primos, chamado de “conjectura fraca”, que estava sem solução desde o século 18.
Vídeos sobre números primos
Para compreender ainda mais o grupo numérico dos números primos, selecionamos alguns vídeos complementares. Confira a seguir:
Concurso Saber Porquê: Qual a relação entre “2, 3, 5, 7, 11…”, um segredo e a Internet?
Este vídeo mostra como os números primos servem para manter a segurança no compartilhamento de dados, revelando curiosidades a respeito do desenvolvimento da criptografia. O vídeo, produzido pela Faculdade de Ciências da Universidade de Lisboa, é narrado em português de Portugal, mas é perfeitamente compreensível.
Números Primos
O professor Ítalo Benfica, do canal Matemática no Papel, relembra a definição de números primos em um vídeo conciso e muito explicativo.
O que são Múltiplos, Divisores e Números Primos
Neste vídeo, o professor Renato Mucciacito, do canal Reducática, explica alguns conceitos importantes para a compreensão dos números primos, então, se você ainda tem dúvidas a respeito de múltiplos e divisores, assista à videoaula acima.








