Noções de geometria plana: forma, perímetro, área, volume e Pitágoras

A geometria é a área da matemática que estuda as figuras geométricas. As noções de geometria são divididas entre o estudo das figuras bidimensionais, chamada de geometria plana, e das figuras tridimensionais, que chamamos de geometria espacial.

As figuras bidimensionais são assim chamadas por possuírem duas dimensões, ou seja, elas têm duas medidas a serem consideradas: comprimento e largura, portanto, planas.

Já as figuras tridimensionais, além do comprimento e da largura, também possuem altura. De modo geral, a geometria espacial estuda o conceito de volume, que é a medida de capacidade dos sólidos geométricos.

Conceitos básicos da geometria plana

A geometria plana foi criada no período da Antiguidade pelo matemático grego Euclides de Alexandria, chamado o “Pai da geometria”. Esta área da matemática utiliza até hoje os princípios e hipóteses criadas por ele. Por isso, a geometria plana também é conhecida como geometria euclidiana.

Quando aprendemos geometria plana alguns conceitos são considerados verdadeiros sem a necessidade de serem provados, chamamos estes conceitos de primitivos ou axiomas. Ou seja, eles são aceitos pela comunidade matemática sem a necessidade de demonstrações.

Os axiomas básicos da geometria são: ponto, reta e plano. Ainda que os conceitos geométricos sejam estabelecidos por meio de definições, as noções primitivas não são, elas precisam ser representadas por meio de exemplificações.

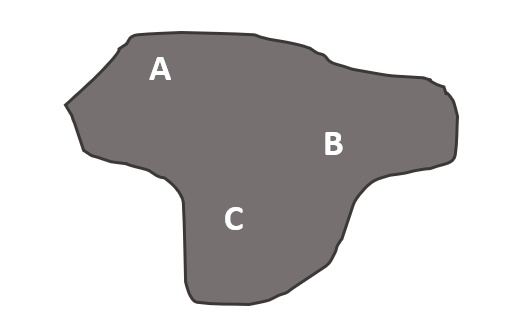
Alguns exemplos de ponto que podemos considerar são: uma estrela, um pingo de lápis, um furo de alfinete. Podemos perceber uma reta em um arame esticado, os lados de uma janela ou as faixas no asfalto. E conseguimos reconhecer um plano em um quadro branco ou uma pizza. Agora, passemos para as definições:

Ponto

Dentro das noções básicas de geometria, o ponto é representado por meio de letras maiúsculas. Segundo Euclides de Alexandria, o ponto é algo que não possui partes nem dimensões. Os pontos são representados pelas letras maiúsculas latinas: A, B, C, D, E etc.

Mas, a fim de aplicar conceito de ponto, analisa-lo e estuda-lo, consideramos as noções de: pontos lineares e semirretas.

• Pontos colineares: são pontos que pertencem a uma mesma reta. Na figura abaixo, os pontos M, N e O são colineares, pois todos pertencem à mesma reta a. Já os pontos da linha F, G e H não são colineares, dado que G não pertence, ou seja, não está inserido na reta b.

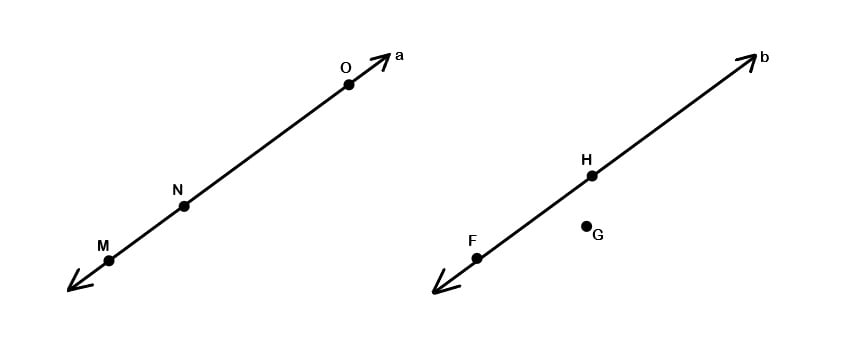
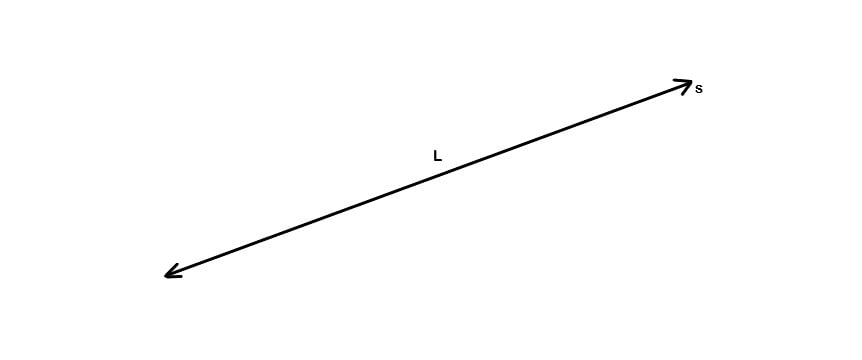
• Semirretas: na figura a seguir um ponto L sobre uma reta s, divide esta reta em duas semirretas. Sendo o ponto L a origem comum das duas semirretas, que são chamadas de semirretas opostas.

Segmentos consecutivos, colineares, congruentes e adjacentes

Considere que temos uma determinada reta r e dois pontos distintos Y e Z sobre a reta, o conjunto de todos os pontos localizados entre Y e Z inclusive os próprios Y e Z, recebem o nome de segmento de reta, neste caso, chamado de YZ.

Dependendo do caso, ao trabalhar com segmentos de reta, é interessante usar dois conceitos: origem, que é o ponto onde o segmento se inicia, e extremidade, que é o ponto onde o segmento termina.

Desse modo, podemos classificar os segmentos de retas em: consecutivos, colineares, congruentes e adjacentes.

• Segmentos consecutivos: consideramos dois segmentos de reta consecutivos quando a extremidade de um deles é também extremidade do outro. Ou seja, uma extremidade de um coincide com a extremidade do outro.
• Segmentos colineares: chamamos de colineares, quando temos dois segmentos de reta que estão em uma mesma reta.

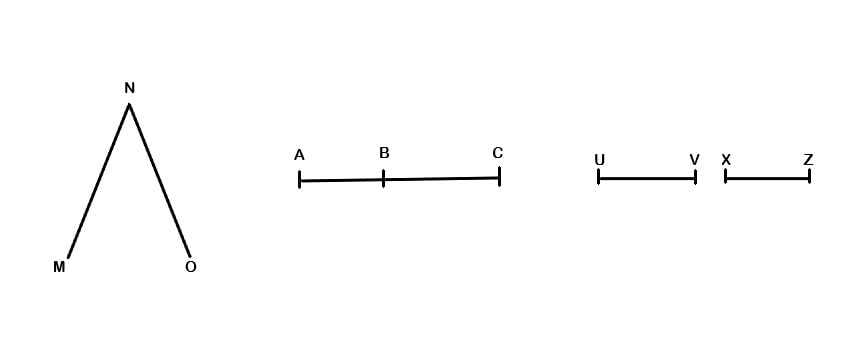
De acordo essa imagem podemos fazer as seguintes considerações:

3. Os segmentos MN e NO são segmentos consecutivos, mas não são colineares.
4. Os segmentos AB e BC são consecutivos e colineares.
5. Os segmentos UV e XZ não são consecutivos, mas, separadamente, cada um é um segmento colinear..

• Segmentos Congruentes: são os segmentos de reta que possuem as mesmas medidas.

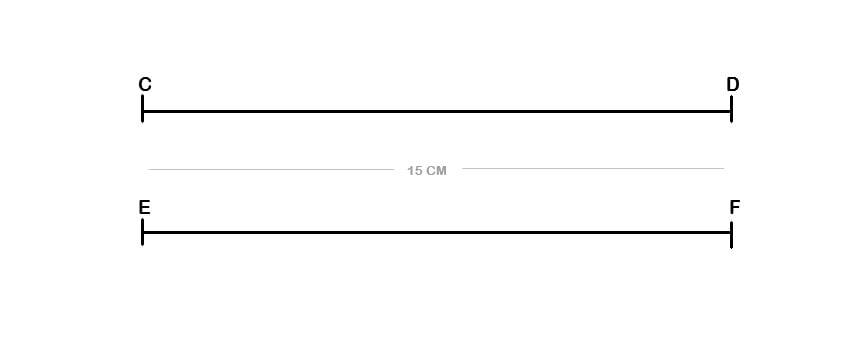
Na figura acima, o segmento de reta CD e EF são congruentes, dado que possuem mesma medida. A congruência entre os segmentos CD e EF é denotada por CD~EF, onde “~” é o símbolo de congruência.

• Segmentos Adjacentes: quando temos dois segmentos colineares e consecutivos consideramos que eles são adjacentes caso possuam, apenas, uma extremidade comum e não compartilhem outro ponto de encontro.

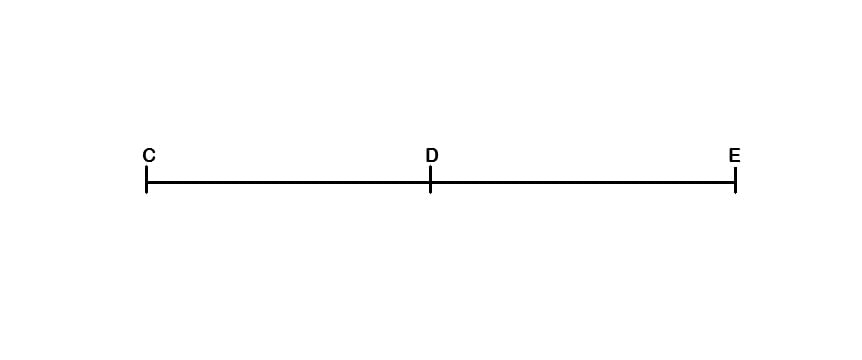
Os segmentos CD e DE são adjacentes, tendo somente D como ponto comum. Já os segmentos CD e DE não são adjacentes, uma vez que há muitos pontos em comum entre eles.

• Ponto médio de um segmento M: consideramos ponto médio do segmento de reta, aquele que o divide em dois segmentos congruentes, que também podemos chamar de ponto de equilíbrio de um segmento de reta.

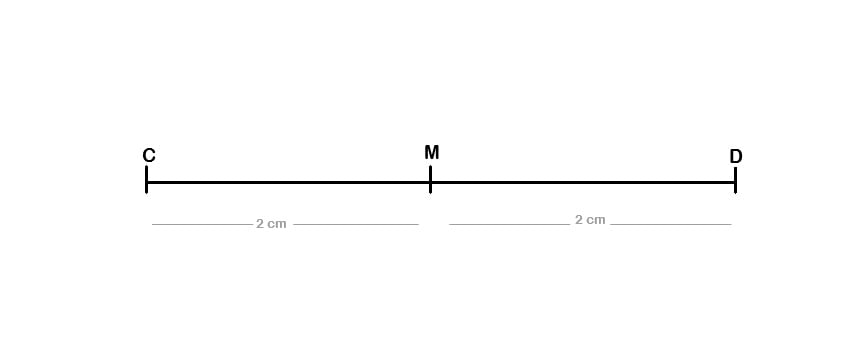
Na figura acima, o segmento de reta CD é dividido pelo ponto M, gerando dois segmentos congruentes, ou seja, CM~MD.

Reta

Chamamos de reta os pontos, que quando conectados, formam uma linha, sem considerar a largura ou o comprimento. Desse modo, a reta é infinita para os dois sentidos. Na linguagem geométrica usamos as letras minúsculas latinas (a, b, c, d etc.) para representar as retas.

Precisamos considerar também o segmento de reta que é a parte de uma reta que está compreendida entre dois pontos da reta, portanto ele é finito, ou seja, possui início e fim. Além disso, o segmento sempre é representado por duas letras maiúsculas com um traço em cima.

Exemplo: temos um segmento de reta s e ele possui dois pontos que podemos representar por A͞B.

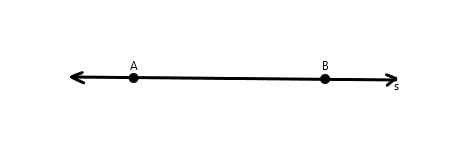
Além disso, temos a semirreta. Ela tem início em um ponto da reta e é infinita para uma das suas direções (ou extremidades). A semirreta é representada na geometria por meio de duas letras maiúsculas com uma seta em cima indicando a direção.

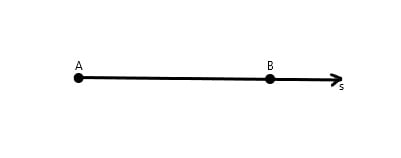
Exemplo: temos uma semirreta s e ela possui dois pontos, onde A é o início e segue em direção ao ponto B, que podemos representar por AB.

Voltando às retas, elas podem ser apresentadas na posição inclinada, vertical e horizontal. Algumas das noções básicas de geometria a respeito da representação das retas em um plano são os conceitos de retas paralelas, concorrentes e perpendiculares.

1. Retas Paralelas: são aquelas que não se cruzam, ou seja, não possuem ponto comum. Além disso, elas estão a uma mesma distância no plano para todos os pontos e pertencem ao mesmo plano (coplanares, ou representação: P), portanto a interseção é vazia: t ∩ p = { }.

A notação para duas retas t e p, que são paralelas, é dada por t||p.

Nota: quando temos duas retas paralelas que pertencem ao mesmo plano e possuem todos os pontos em comum, chamamos elas de retas coincidentes.

2. Retas concorrentes: quando duas retas se possuem um único ponto em comum, ou seja, elas se cruzam, têm um ponto de intersecção.

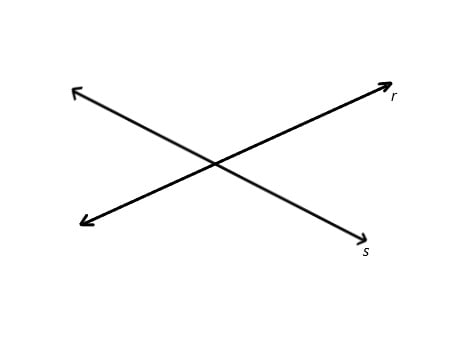
A notação para duas retas r e s que são concorrentes é dada por r X s.

3. Retas Perpendiculares: são duas retas concorrentes que possuem um ponto comum, no qual é formado um ângulo de 90 graus, ou ângulo reto. A fim de apontar que as retas são paralelas é usada a notação a b.

Outra propriedade da reta perpendicular que podemos observar na figura abaixo: quando temos um ponto localizado fora da reta dada, ela pode ser traçada apenas uma reta perpendicular, observe:

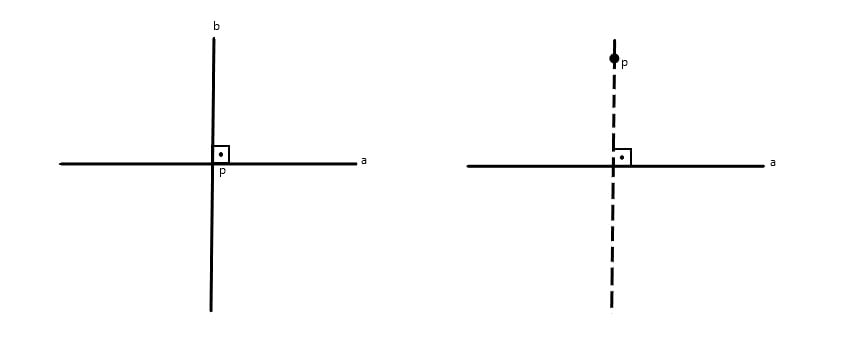
4. Retas transversais e ângulos especiais: são retas transversais aquelas que “atravessam” ou “cruzam” com outras retas é fazendo com elas intersecções em pontos diferentes.

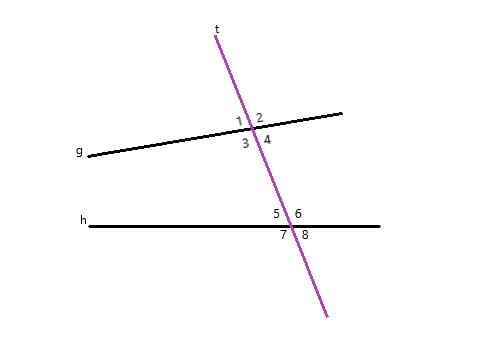
Na imagem acima temos a reta t, que é transversal às retas g e h. Estas três retas formam 8 ângulos, sendo que os ângulos 3, 4, 5 e 6 são ângulos internos e os ângulos 1, 2, 7 e 8 são ângulos externos.

Cada par destes ângulos recebe nome de acordo com a localização em relação à reta transversal e às retas g e h, entenda:

• Ângulos Correspondentes: são aqueles que estão do mesmo lado da reta transversal. Sendo um deles interno e o outro externo. De acordo com o exemplo acima, os pares são: (1,5), (2,6), (3,7), (4,8), (1,5), (2,6), (3,7), (4,8).
• Ângulos Alternos: são os que estão em lados opostos da reta transversal. Ambos são considerados externos ou internos. Segundo a figura acima, os pares são: (1,8), (2,7), (3,6), (4,5), (1,8), (2,7), (3,6), (4,5).
• Ângulos Colaterais: são aqueles que estão do mesmo lado da reta transversal. Podendo ambos serem externos ou internos. Os pares são: (1,7), (2,8), (3,5), (4,6), (1,7), (2,8), (3,5), (4,6).

Propriedades das retas transversais

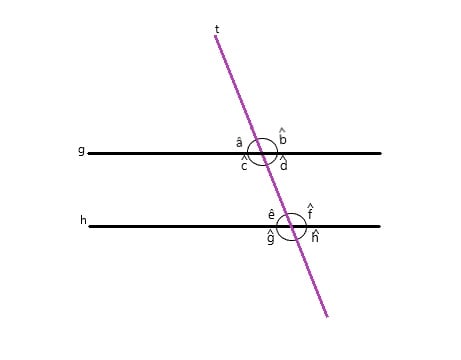
A fim de entender as propriedades das retas transversais vamos considerar a imagem acima. Quando temos duas retas paralelas cortadas por uma reta transversal (em cor violeta), os ângulos correspondentes (c, e) e os ângulos alternos internos (c, f) são congruentes, ou seja, tem as mesmas medidas.

Desse modo, também podemos considerar que os ângulos d, e, h são congruentes.

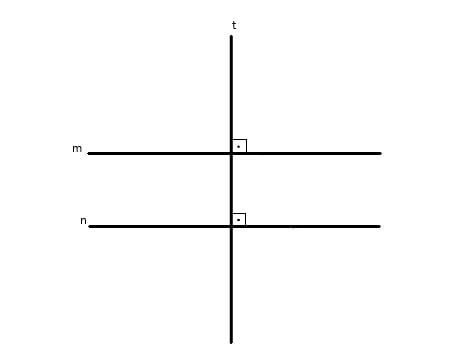
Agora, quando analisamos duas retas paralelas m e n e uma reta transversal t, que é perpendicular a uma das retas paralelas, logo ela também vai ser perpendicular à outra. Veja na figura a seguir.

Plano

De acordo com as noções básicas de geometria plana, consideramos como plano algo que é formado por uma superfície que possua todos os pontos e retas. O plano tem duas dimensões: comprimento e largura. É representado na geometria por letras do alfabeto grego (α, β, γ, δ, θ, λ etc.).

Posição relativa entre reta e plano

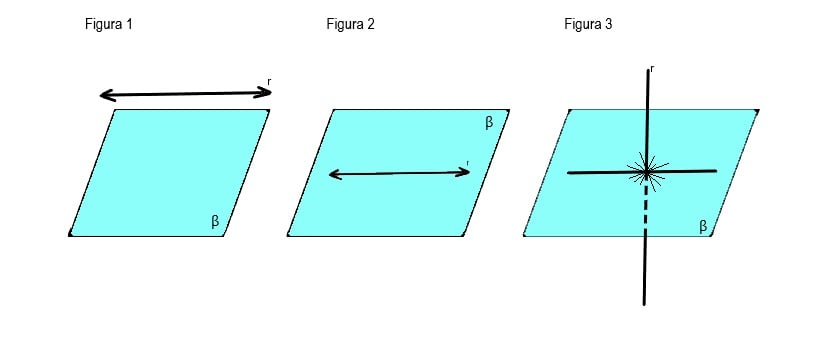
Quando observamos estas três figuras, podemos considerar que uma reta e um plano podem ter as seguintes posições relativas:

Figura 1. Temos uma reta s que é paralela ao plano β (beta). Podemos afirmar que são paralelas dado que eles não têm nenhum ponto em comum.

Figura 2. Nos apresenta uma reta s contida no plano β (beta). Essa afirmação é possível uma vez que todos os pontos infinitos da reta s pertencem ao, ou seja, estão dentro do plano β (beta).

Figura 3. Retas e planos secantes ou concorrentes: a reta t será concorrente ao plano β se possuírem um ponto em comum.

Posição entre dois planos

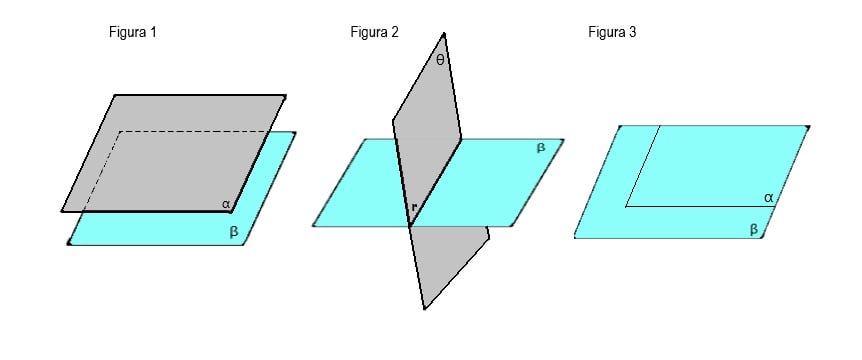
Vamos considerar estas três figuras, para entender as posições relativas que dois planos podem ter entre si:

Figura 1. Temos dois planos paralelos, uma vez que ambos possuem pontos em comum. Caso tenhamos uma reta que pertence ao plano α (alfa) e ela for paralela a uma reta pertencente ao plano β (beta).

Figura 2. Temos representado planos secantes, o plano θ (ômega) é distinto ao plano β (beta) e a intersecção (lugar onde os planos se cruzam) entre eles formar uma reta r.

Figura 3. Nos apresenta planos coincidentes, temos um plano α (alfa) e um plano β (beta) que são equivalentes a um mesmo plano. Em outras palavras, todos os pontos infinitos de alfa e beta pertencem ao outro.

Ângulos

Outro conceito básico da geometria é a noção de ângulo que compreende a região entre dois segmentos de retas que têm um mesmo ponto em comum. Ou seja, o ângulo é a medida da abertura entre estes seguimentos. Eles podem ser medidos em graus ou radianos e são classificados de acordo com sua medida:

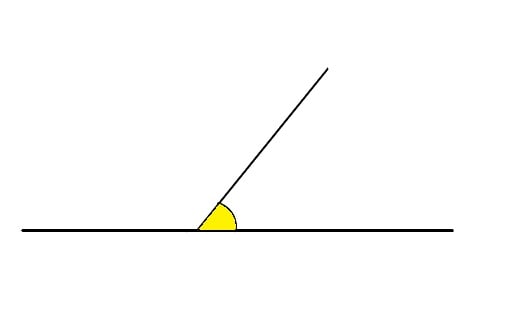
• Ângulo agudo é aquele com medida menor que 90° (0° < α < 90°).

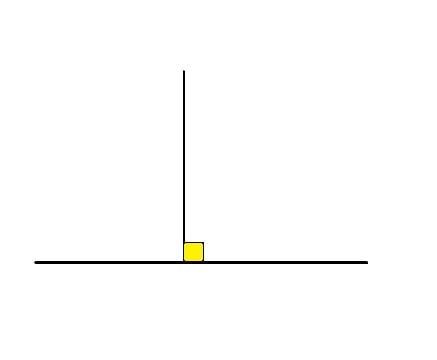
• Ângulo reto é aquele que tem medida igual a 90°.

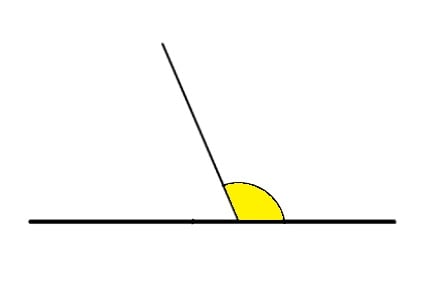
• Ângulo obtuso é aquele com medida maior que 90° (90° < α < 180°).

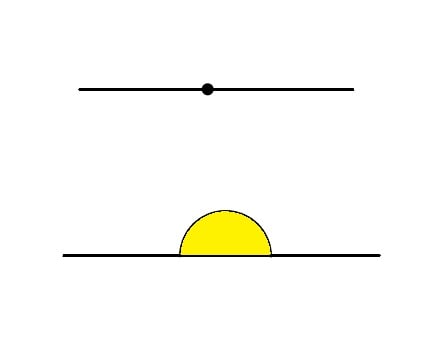
• Ângulo raso tem medida igual a 0° ou 180°.

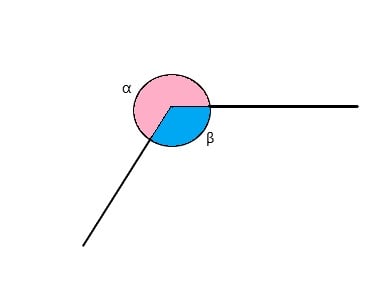
• Ângulo Côncavo é aquele que tem medida entre 180° e 360°.

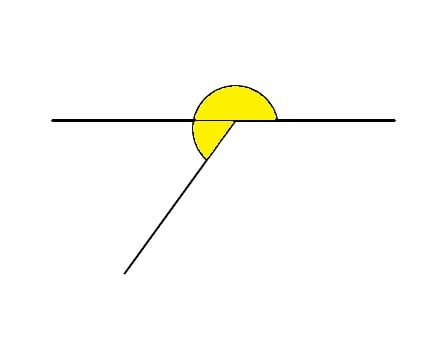
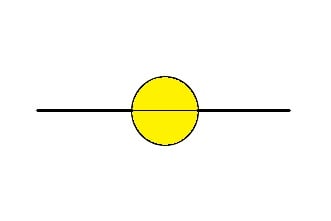
• Ângulo completo ou de uma volta é aquele que possui medida igual a 360°.

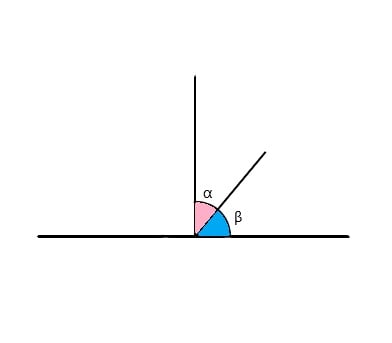
• Ângulos complementares são aqueles que quando somados o resultado é 90° (α+β=90).

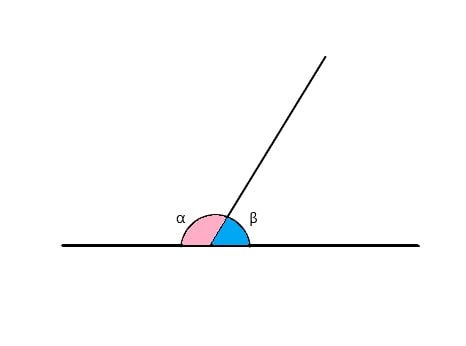
• Ângulos suplementares são aqueles que quando somados o resultado é igual a 180° (α+β=180).

• Ângulos replementares são aqueles que quando somados o equivalente é igual a 360° (α+β=360).

Formas geométricas planas

Outro conceito que estudamos dentro das noções básicas da geometria plana são os polígonos, que compreende as figuras planas e fechadas. Entre os principais polígonos temos: triângulo, quadrado, retângulo, círculo, circunferência, trapézio, paralelogramo e losango.

Alguns polígonos são nomeados de acordo com o número de lados que eles possuem, como: triângulo (3 lados), quadrilátero (4 lados), pentágono (5 lados), hexágono (6 lados), heptágono (7 lados), octágono (8 lados), eneágono (9 lados), decágono (10 lados), undecágono (11 lados), dodecágono (12 lados), pentadecágono (15 lados), icoságono (20 lados).

Representamos os planos por meio das letras gregas minúsculas (α, β, γ etc.). Agora vamos conhecer um pouco mais sobre as especificidades de alguns polígonos.

Triângulo

O triângulo é um polígono formado por três lados. Os lados dessa figura geométrica plana são segmentos de retas unidos nos vértices. Ele pode ser classificado de acordo com o número de lados ou ângulos internos, veja:

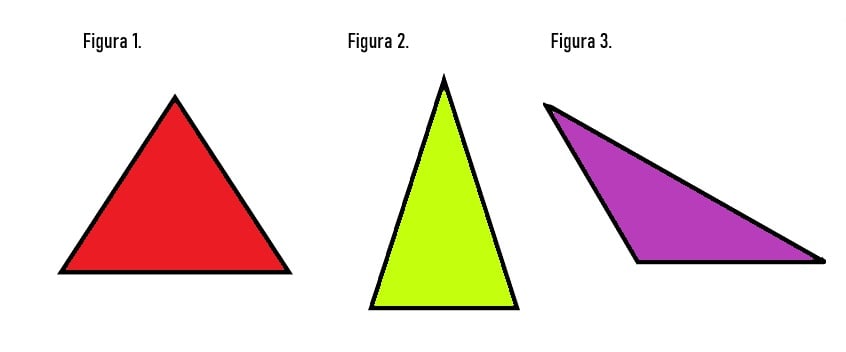
Figura 1. Temos um triângulo equilátero, ou seja, todos os lados e ângulos internos deste polígono são congruentes;

Figura 2. Observamos a representação de um triângulo isósceles, este polígono de três lados possui dois lados e dois ângulos internos congruentes;

Figura 3. Temos um triângulo escaleno, no qual todas as medidas internas são diferentes.

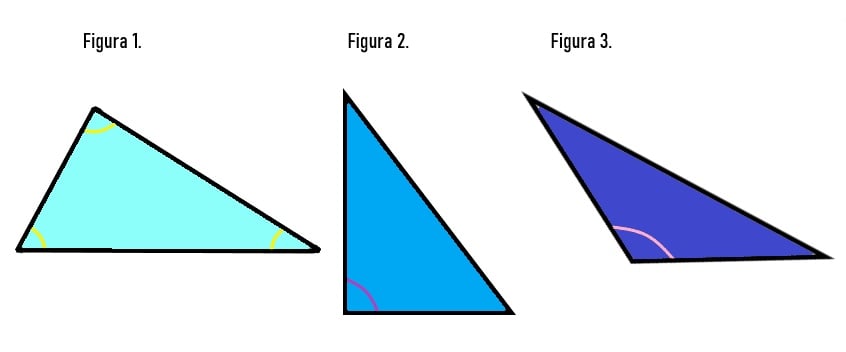
Figura 1. Observamos um triângulo acutângulo, ele possui todos os ângulos internos menores que 90°;

Figura 2. Podemos observar um triângulo retângulo, este polígono de três lados possui um ângulo de 90°;

Figura 3. Temos um triângulo obtusângulo, ele recebe este nome por possuir um ângulo interno obtuso, ou seja, maior que 90°.

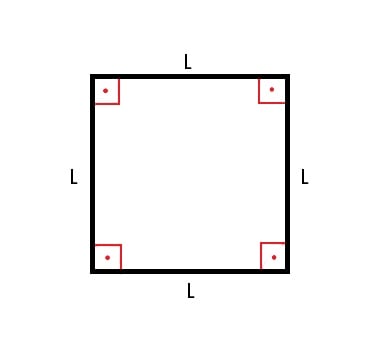
Quadrado

Chamados de quadrado o paralelogramo (figura plana de lados paralelos) formado por quatro lados e que possui todos os ângulos internos congruentes (iguais) e retos, ou seja, de 90°.

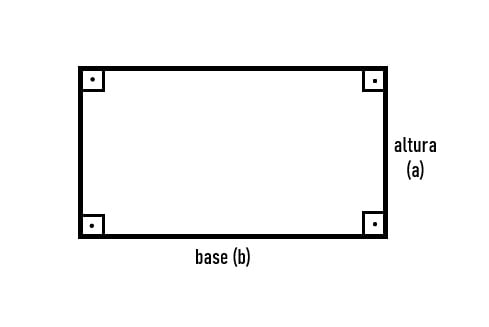
Retângulo

Quando temos um paralelogramo com lados dois a dois congruentes e paralelos, damos a esta figura geométrica plana o nome de retângulo. Seus ângulos internos são congruentes e retos.

Círculo e circunferência

Segundo a geometria plana, chamamos de círculo ou disco (figura 1), uma figura plana que seja limitada pela circunferência e que corresponde ao espaço interno formado pelo conjunto de todos os pontos do plano.

Já a circunferência (figura 2) é formada por um conjunto de pontos que possuem a mesma distância do centro que tem valor equivalente a medida do raio

Trapézio

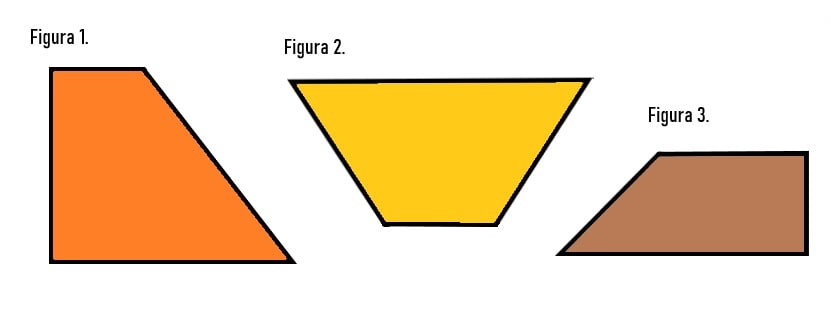
Quando temos um polígono formado por duas bases paralelas com medidas diferentes, damos a ele o nome de trapézio. Ele pode ser classificado segundo a medida dos lados e ângulo internos em:

Figura 1. Trapézio Retângulo: este polígono dois ângulos internos de 90°;

Figura 2. Trapézio Isósceles: quando os lados que não são bases são congruentes (iguais);

Figura 3. Trapézio Escaleno: quando todos os lados têm medidas diferentes.

Losango

Quando estudamos na geometria plana um paralelogramo formado por quatro lados, com lados opostos paralelos e lados e ângulos congruentes (iguais) temos então um losango.

Perímetro e área

Outro conceito básico da geometria plana é a noção de perímetro. Para descobrir o valor do perímetro do qualquer um dos polígonos que mostramos anteriormente basta fazer a soma das medidas de todos os lados dessas figuras geométricas. Em outras palavras, o perímetro é a medida do comprimento de um contorno de uma figura plana.

Quando falamos de área, tramamos da medida usada para estabelecer o tamanho da superfície de uma figura. A fim de fazer o cálculo da área usamos as medidas de comprimento e largura das figuras geométricas (ou polígonos).

 Observe a seguir as fórmulas para o cálculo do perímetro e área das principais figuras geométricas planas:

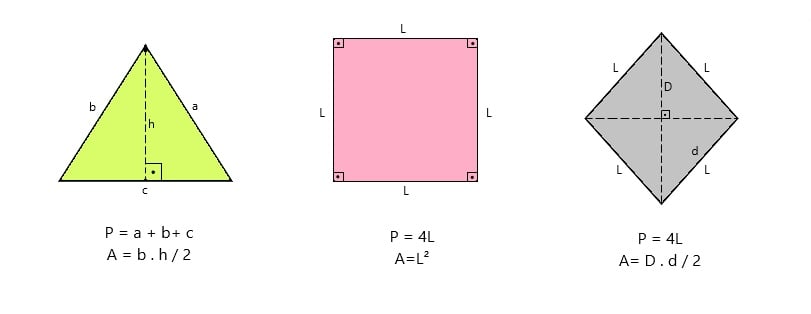
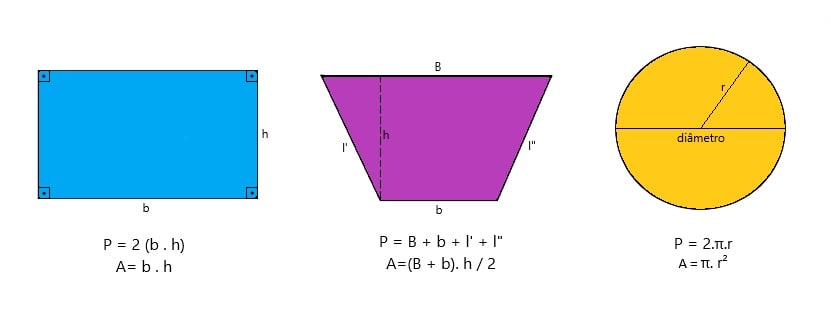
Legenda

P = perímetro
A = área
L = lado
h = altura
abc = lado qualquer
D = diagonal maior
d = diagonal menor
B = base maior
b = base menor
l’ = lado 1
l” = lado 2
r = raio (diâmetro = 2 . r)
π (pi minúsculo) = 3,14
/ = dividido por / sobre

Teorema de Pitágoras

Um último acréscimo ao conteúdo das noções básicas de geometria plana é o teorema de Pitágoras, que relaciona todos os lados de um triângulo retângulo.

A fim de aplicar o teorema, primeiramente é necessário compreender os nomes que o matemático Pitágoras deu a cada um dos lados do triângulo retângulo.

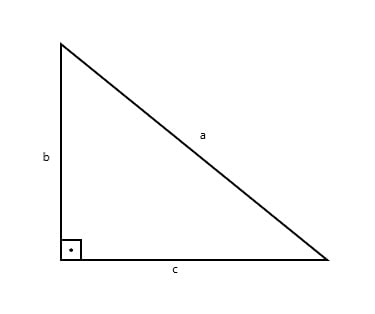
O maior lado, recebe o nome de hipotenusa e ele será sempre oposto ao ângulo reto, que é o ângulo de 90°. Representamos a hipotenusa pela letra a. Os outros dois lados do triângulo são chamados de catetos e são representados pelas letras b e c.

O enunciado do Teorema de Pitágoras é o seguinte: “Em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos”. Que em linguagem matemática é expresso por: a² = b² + c²

Veja a representação desse triângulo na figura a seguir:

Vídeos de apoio