Os números naturais surgiram de um processo natural da humanidade de contar objetos e seres ao seu redor. Os números fracionários, por sua vez, foram estabelecidos para contar as partes de um objeto, uma vez que o todo pode ser dividido em infinitas frações. Os números naturais e fracionários são conceitos antigos da matemática.
Provavelmente a definição de número foi uma das primeiras da matemática a serem assimiladas pelos seres humanos para que o processo da contagem pudesse ser feito.
Segundo a História, por volta de 4.000 a.C, as aldeias situadas às margens dos rios foram se transformando em cidades e, com esse avanço, novas atividades foram surgindo, tornando a vida mais complexa, principalmente com a chegada do comércio.
Como consequência deste desenvolvimento, nasceu também a escrita e, a partir dela, a humanidade passou a representar as quantidades através dos símbolos, chamados de numerais.
O número “um” passou a ser representado pelo numeral “1”, o número “dois” pelo “2”, o “três” pelo “3”, e assim por diante.
Números naturais
Os números, no geral, são elementos abstratos da matemática estabelecidos para descrever quantidade, ordem ou medida. Um rio, dois peixes, três frutas… Infinitos elementos que precisam ser categorizados de acordo com a sua quantidade.
Assim nasceram os números naturais: da necessidade do homem de contar e organizar os elementos a sua volta. Como o próprio nome já diz, o conjunto dos números naturais está “naturalmente” no nosso cotidiano.
Trabalhamos todos os dias com os números naturais, quase que inconscientemente. As suas representações, entretanto, não são tão simples e passam por regras e parâmetros de diferenciação.
O que são os números naturais?
Os números naturais são representados pelo 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …, até o infinito. Pense no maior número que você consegue imaginar! Pensou? Agora pense no sucessor dele. Agora já temos um número maior do que o anterior.
Por isso, diz-se que os números naturais são, de fato, infinitos. Se por um lado conhecemos o seu princípio, sendo ele o 0 ou o 1, é impossível delimitar o fim deste conjunto, ficando o sistema em aberto ao infinito e além!
Os números naturais também são conhecidos como algarismos indo-arábicos. Isso porque os árabes, no século VI, invadiram a Índia e difundiram o seu sistema numérico.
Embora o zero não seja um número natural, no sentido de que não é utilizado para contagem, iremos considerá-lo como um número natural, uma vez que ele possui as mesmas propriedades algébricas que os números naturais.
Evoluindo de uma casa vazia, ou um espaço em branco, o zero se transformou com os hindus na montagem do sistema posicional, suprindo a deficiência da expressão de nulidade.
No ensino básico da matemática, aprendemos a incluir o zero dentro do conjunto dos números naturais. Mas, a partir do ensino superior, passamos a estudar esse conjunto a partir do número 1.
Assim, dentro do estudo básico iremos considerar o zero dentro do nosso conjunto de números naturais.
Conjunto dos números naturais
O conjunto dos números naturais é indicado pela letra maiúscula N e é representado por todos os números inteiros e positivos que se agrupam num conjunto ilimitado de elementos.
N = {0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11,12,13,14,15…}
Quando tiramos o zero desse conjunto obtemos um subconjunto denominado de números naturais não-nulos, que é indicado pela letra maiúscula N seguida do símbolo do asterisco (*), portanto:
N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11,12,13,14,15…}
Sucessor de um número natural
Os sucessores, também chamados de sucessivos ou consecutivos, são os números naturais somados a “1”. Assim, o sucessor de um número natural será sempre maior do que o seu antecessor.
Além disso, todo número natural tem apenas um único número natural sucessor. Por exemplo, o “3” é o único sucessor do “2” e o “4” é o único sucessor do “3”.
Números diferentes têm sucessores diferentes e eles não se repetem. Se o “6” é sucessor do “5”, não tem como o “6” ser sucessor do “4”.
Assim, voltamos à primeira regra: cada número natural tem apenas um único sucessor, que não pode ser substituído.
Devemos observar ainda que, dentro deste conjunto, há apenas um único número que não é sucessor de nenhum outro. Como incluímos o “0”, ele é o numeral sem sucessor, sendo o princípio do nosso conjunto de números naturais.
Antecessor de um número natural
Os números antecessores, também conhecidos por antecedentes ou precedentes, serão sempre menores que os seus sucessores. Da mesma maneira, os números naturais têm apenas um único número antecessor.
Por exemplo, o “2” é o único antecessor do “3” e o “4” é o único antecessor do “5”.
Números diferentes também possuem antecessores diferentes, que nunca poderão ser substituídos, ou seja, eles não se repetem. Se o “5” é antecessor do “6”, não é possível que o “5” seja antecessor do “4”.
Desta feita, existe apenas um único número que não é antecessor de nenhum outro. Considerando o “0” dentro do nosso conjunto de números naturais, e sendo ele a origem do sistema, ele é o único que não possui um antecessor.
Números naturais pares e ímpares
Os números pares são todos aqueles que, ao serem divididos pelo número dois, resultam em um número inteiro. Se o resultado, por sua vez, for um número decimal, diz-se que esse número é ímpar.
Dentro do estudo básico, podemos delimitar que os números pares são aqueles terminados em 0, 2, 4, 6 ou 8, enquanto os ímpares são aqueles que não são pares e são terminados em 1, 3, 5, 7 ou 9.
Na definição científica, entende-se que todo número par é múltiplo de 2 e que todo número ímpar não é múltiplo de 2. Além disso, todo número par é divisível por 2 e todo número ímpar não é divisível por 2.
Se os números inteiros são formados por números negativos, positivos e não-decimais, incluindo o 0, destaca-se que os números naturais agrupam apenas os números inteiros, positivos e não-decimais.
A partir deste critério, compreendemos que os números inteiros contêm os números naturais, que por sua vez, contém o subconjunto dos números naturais ímpares ou pares, a depender dos critérios estabelecidos pelo subconjunto.
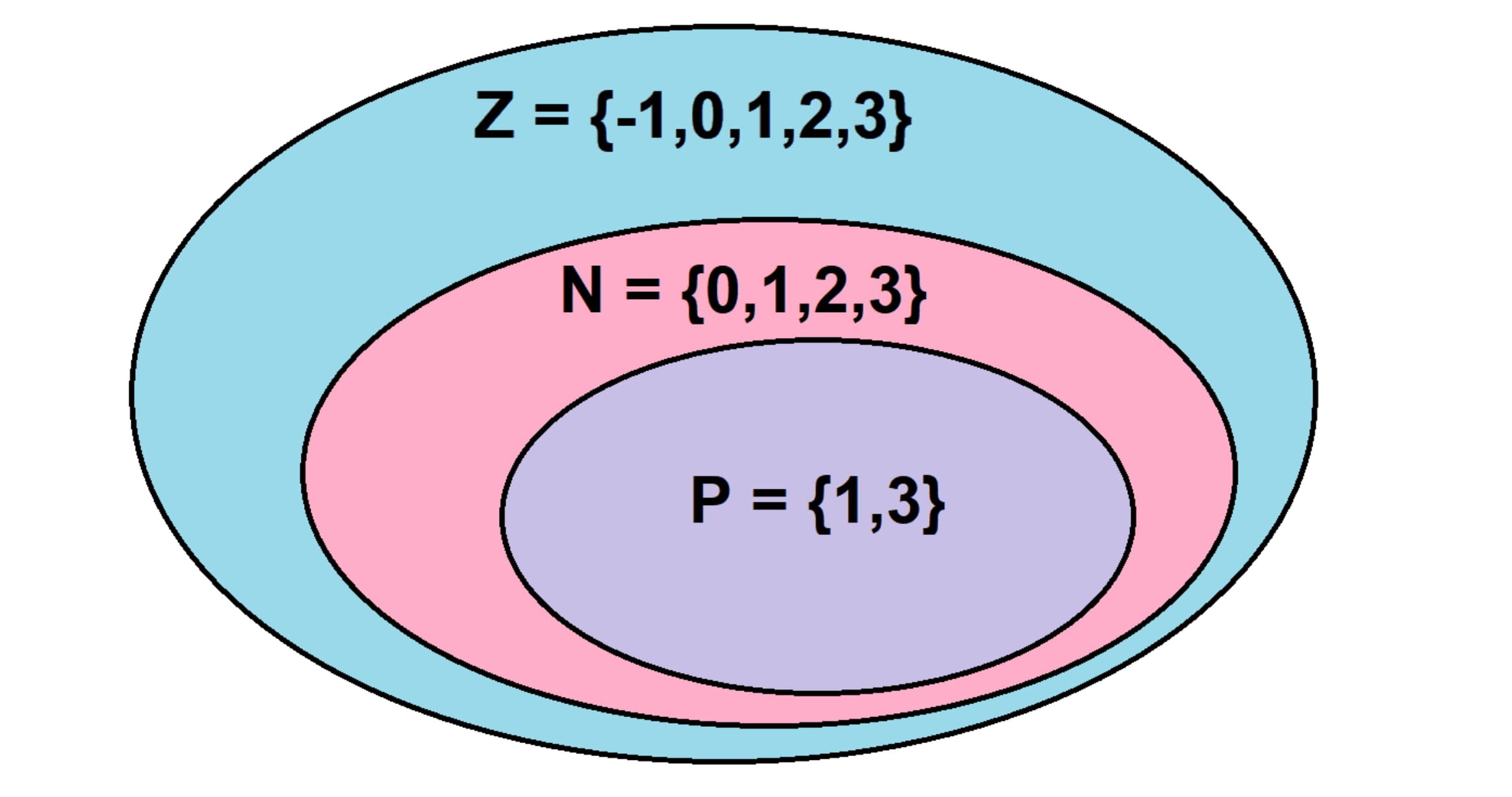
O exemplo demonstra que um conjunto de números inteiros definidos por Z, agrupa em seu interior o subconjunto dos números naturais, delimitados por N, que por sua vez, reúne em P os números naturais ímpares.
Subconjunto dos números naturais
Todo conjunto numérico reúne números que apresentam uma ou mais similaridades entre si. Dentro de todo conjunto numérico encontramos os subconjuntos.
Os subconjuntos dos números naturais são conjuntos que agrupam números com alguma similaridade entre si, sendo que as características em comum são previamente determinadas a partir de uma condição que aproxime os elementos.
Dentro do universo dos números naturais podemos estabelecer diversos critérios para criar um subconjunto, por exemplo, que contenha apenas os números naturais ímpares, menores a 15.
Assim: A = {1,3,5,7,9,11,13,15}
Em uma ilustração, também podemos exemplificar a criação de um subconjunto de números naturais pares dentro do conjunto dos números naturais. Observe:
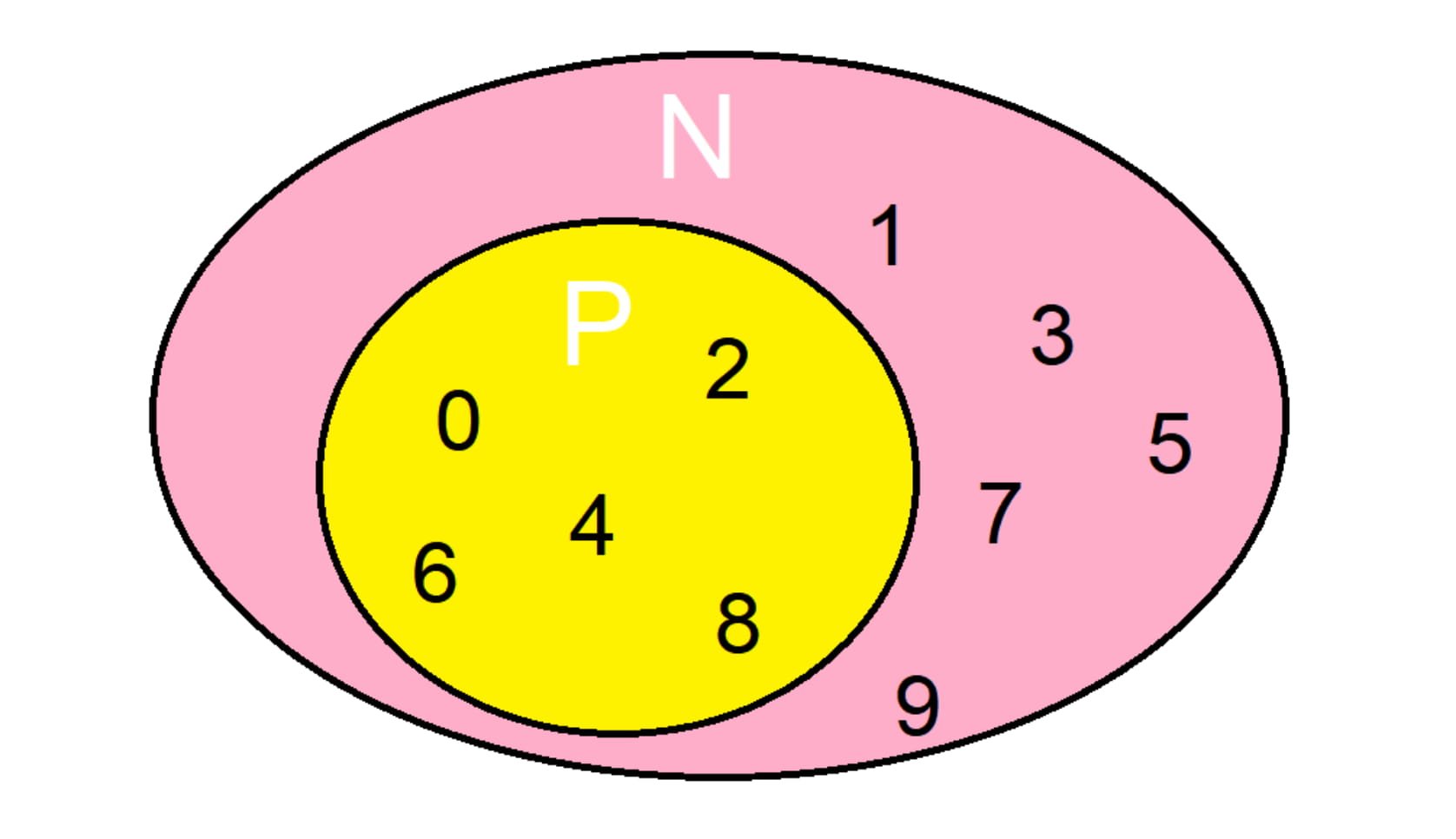
Ex: Pelo desenho, concluímos que o conjunto dos números naturais pares é um subconjunto de N.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
P = {0, 2, 4, 6, 8}
Assim: P ⊂ N, que se lê: “P está contido em N” ou N ⊃ P, que significa “N contém P”.
A seguir, é possível conferir alguns símbolos básicos utilizados para representar os conjuntos e suas relações com subconjuntos.
- A: Nome do novo conjunto, que pode ser qualquer letra maiúscula do alfabeto;
- { : Delimita o conjunto;
- x : Um número, podendo ser qualquer letra minúscula do alfabeto;
- ∈ : Pertence;
- ∉ : Não pertence;
- ⊃ : Contém;
- ⊂ : Está contido;
- | : Tal que;
- > : Maior que;
- < : Menor que;
- ≥ : Maior ou igual que;
- ≤ : Menor ou igual que;
- + : Positivo
- – : Negativo
- ≠ ; Diferente;
- “condição”: Condição para formar o novo conjunto, por exemplo: x é ímpar, x > 2, x ≤ 9, etc.
- Z = Números Inteiros
- N = Números Naturais
Operações com número naturais
Com os números naturais é possível realizar diversas operações matemáticas, como adição, subtração, multiplicação e divisão.
Adição
Na adição, a soma de dois números naturais resultará sempre em outro número natural. Nesta operação teremos “a + b = c”, sendo “a” e “b” as parcelas da soma e “c” o total da operação.
Por exemplo, 4 + 2 = 6. É importante notar que a ordem dos números não influenciará no resultado, assim, 2 + 4 = 6.
Já o zero, no conjunto dos números naturais, é chamado de elemento neutro. Portanto: 5 + 0 = 5 ou 0 + 7 = 7.
Exercício: A partir da explicação acima, tente resolver o problema matemático a seguir:
Helena tinha um saldo de R$ 2.574,00 na sua caderneta de poupança. No último trimestre, recebeu R$ 1.687, 00 de juros e correção monetária. Com que saldo ficou?
2.574 + 1.687 = ?
Solução: Para resolver este problema iremos somar 2.574 a 1.687, resultando em 4.261. No total, Helena ficou com um saldo de R$ 4.261,00.
Subtração
Na subtração, retiramos uma quantidade de outra, e o valor restante dará o resultado dessa operação, que pode ser representada por “a – b = c”.
É importante ressaltar que o resultado na subtração nem sempre resultará em um número natural, podendo ele ser negativo, o que não se enquadra na regra dos números naturais, sempre positivos.
Ademais, na subtração a ordem dos números também influenciará no resultado. Exemplo:
5 – 3 = 2 (número natural)
3 – 5 = -2 (número não-natural, negativo)
Exercício: A partir da explicação, tente resolver o problema matemático abaixo:
O número da casa de Ana é 2021 e o número da cada de Marcela é 2000. O número da casa de André corresponde a diferença entre o número da casa de Ana e o número da casa de Marcela. Qual é o número da casa de André?
2021 – 2000 = ?
Solução: Para resolver este problema iremos subtrair 2000 de 2021, resultando em 21. O resultado mostra que o número da casa de André é 21.
Multiplicação
A multiplicação dos números naturais, assim como na adição, sempre resultará em um produto de número natural, podendo ser representada por a x b = c.
Esta operação pode ser explicada pela adição de parcelas iguais. Ao invés de somarmos 5 + 5 + 5 = 15, podemos calcular 5 x 3 = 15.
Da mesma maneira, cinco vezes o número 100, por exemplo, seria o mesmo que somar 100 + 100 + 100 + 100 + 100.
Na multiplicação, a ordem dos fatores também não afetará o resultado do produto. Todo número multiplicado pelo zero resultará em zero. E o número 1, nesta operação, é considerado o elemento neutro, não afetando no resultado do produto.
Assim:
9 x 1 = 9 e 1 x 9 = 9
9 x 0 = 0 e 0 x 9 = 0
Exercício: A partir da explicação, tente resolver o problema matemático sugerido:
O edifício comercial Monte Serrat possui 30 andares. Em cada andar, há 10 salas. Quantas salas existem na torre, no total?
30 x 10 = 300
Solução: Para resolver este problema iremos multiplicar o número de andares pela quantidade de salas de cada andar. O resultado total mostra que o edifício comercial Monte Serrat possui 300 apartamentos no total.
Divisão
A divisão, por fim, é uma operação inversa à multiplicação. Nessa operação, repartimos uma quantidade total em partes iguais. Sendo a ÷ b = c.
O produto deste fracionamento poderá ser um número inteiro, positivo, e, portanto, um número natural.
Dizemos que uma divisão é exata quando não sobram restos. Se temos 3 laranjas e elas serão divididas entre três pessoas, cada um ficará com uma laranja, não sobrando nenhum resto na divisão.
Por outro lado, se temos 4 livros para ser divididos entre 3 crianças, cada uma ganhará 1 livro, restando ainda um, que será deixado de lado, para que todas as crianças sejam contempladas igualmente, não favorecendo nenhuma.
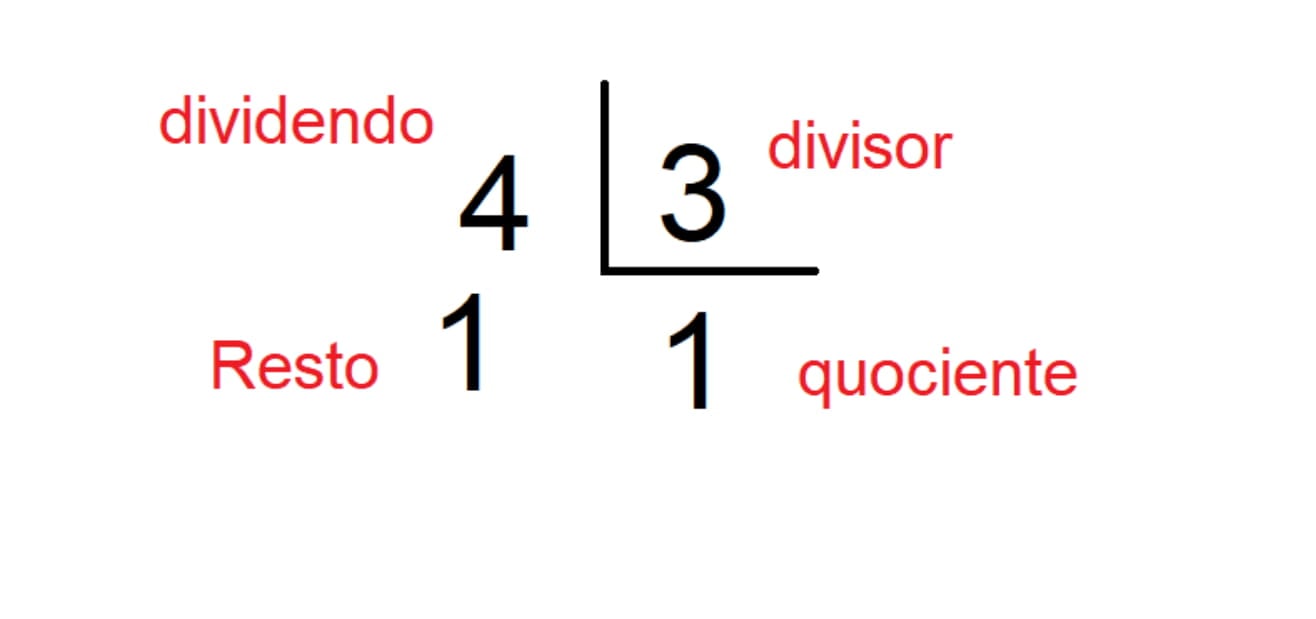
No entanto, quando o dividendo for menor do que o divisor, o quociente será um número decimal, com vírgulas, o que não se enquadra dentro do conjunto dos números naturais.
Além disso, é preciso reforçar que nesta operação, assim como na subtração, a ordem dos fatores irá influenciar no resultado do produto. A divisão pelo número 0 é indefinida ou impossível. E a divisão por 1, sempre resultará no próprio dividendo. Assim:
- 10 ÷ 1 = 10
- 10 ÷ 0 = Impossível
- 10 ÷ 5 = 2 (número natural)
- 5 ÷ 10 = 0,5 (número decimal)
Exercício: A partir da explicação, tente resolver o problema a seguir:
Joana comprou 65 chocolates e quer dividir igualmente os doces entre seus 5 sobrinhos. Quantos chocolates cada sobrinho de Joana irá ganhar?
65 ÷ 5 = ?
Solução: Para resolver este problema iremos dividir 65 chocolates entre as cinco crianças. O resultado correto irá repartir igualmente 13 chocolates para cada uma das 5 crianças.
Para confirmar o resultado também podemos seguir a ordem inversa, da multiplicação. Se cada uma das 5 crianças ganhou 13 chocolates, podemos calcular 13 x 5 = 65, o que mostrará o total de chocolates comprados e divididos por Joana.
Números Fracionários
Diferentemente dos números naturais, os números fracionários não são números inteiros e podem ser definidos como aqueles que representam uma ou mais partes de um total.
Ao dividirmos um objeto em um determinado número de partes, cada conjunto desses fragmentos representará um número fracionado do todo.
Um exemplo bastante utilizado para ilustrar os números fracionários é a pizza. Uma pizza de tamanho grande, geralmente repartida em 8 partes, facilita a divisão igualitária entre os indivíduos.

Cada um desses pedaços representa uma parte do todo. Assim, 1 de 8 é um número fracionário e pode ser representado por
1/8
Por esta representação entendemos que apenas um pedaço de pizza foi retirado do total. Se mais um pedaço da pizza for consumido, então a fração passará a ser de
2/8
E assim sucessivamente, até que os oito pedaços de pizza sejam completamente consumidos, voltando ao todo, que é
8/8
Ou seja, 1 pizza completa.
O que são os números fracionados?
Os números fracionários são aqueles que representam uma ou mais frações de uma unidade dividida em partes iguais. Eles também representam as divisões e se referem ao fracionamento das partes de um todo, 1 unidade.
Os números fracionários são representados por dois números inteiros (termos da fração) separados por um traço horizontal (traço de fração).
O número de cima (numerador) pode ser qualquer número inteiro e o número de baixo (denominador) deverá ser diferente de zero.
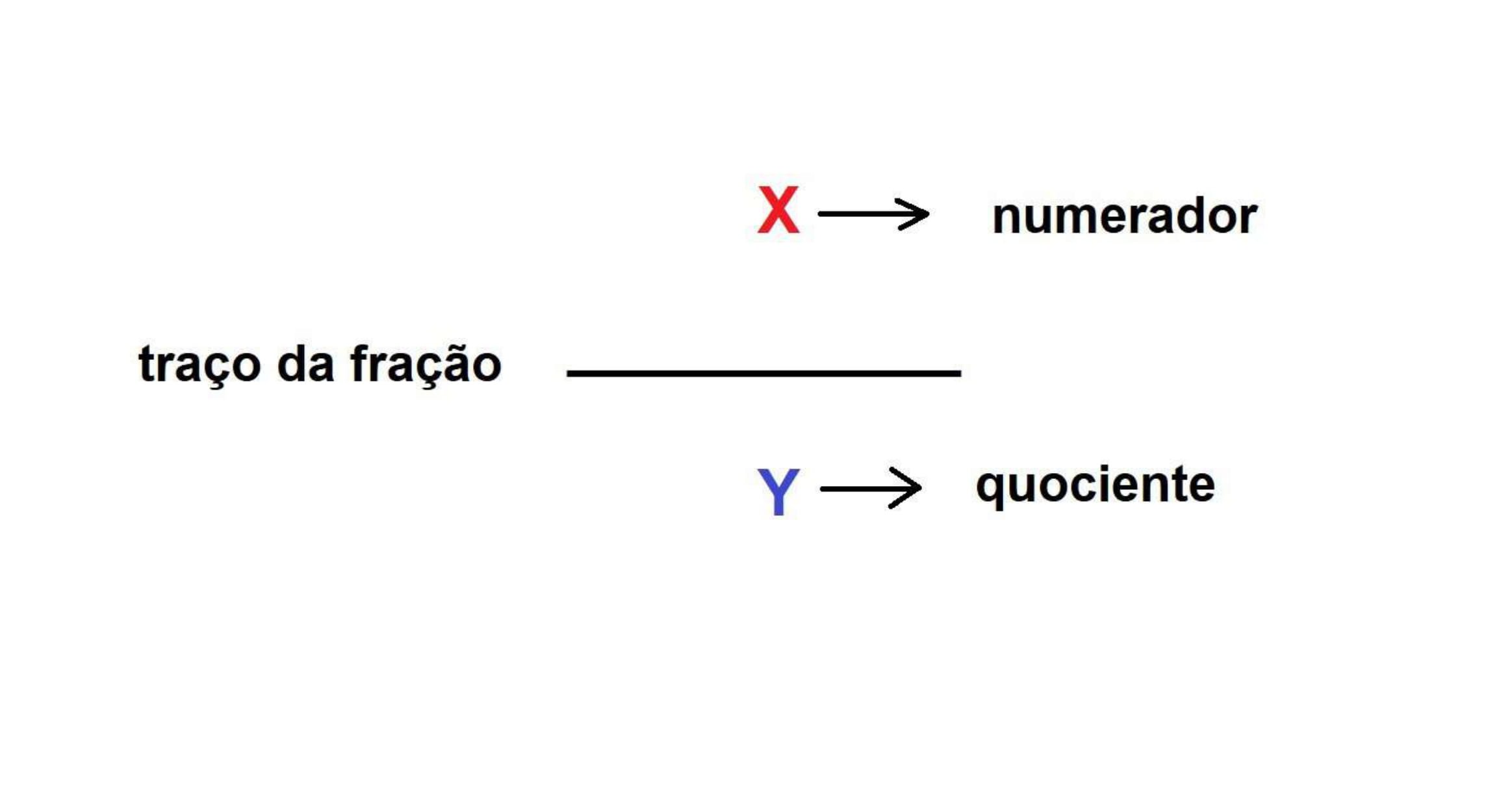
O número fracionário ½, por exemplo, significa que um inteiro (numerador) foi dividido em duas partes iguais (denominador). Assim, o resultado é meio ou a metade do todo.
Leitura de números fracionados
Embora os números fracionários sejam utilizados majoritariamente na matemática, o seu emprego também pode ser encontrado com recorrência nas áreas administrativas, financeiras e na linguagem corrente.
Quando dizemos que percorremos a metade de um trajeto, por exemplo, significa que estamos fracionando em duas partes iguais a distância total de um itinerário.
Os numerais fracionários são flexionados em gênero (masculino e feminino) e número (singular e plural) conforme o numeral cardinal que os antecedem. Como por exemplo:
- Já andamos um terço do caminho.
- Os convidados já devoraram meio bolo.
- Falta pagar apenas o duodécimo do salário do funcionário.
A palavra avo, usada apenas nos denominadores maiores do que dez, é um substantivo masculino. Quando a palavra está justaposta ao denominador de uma fração, indica a quantidade de vezes em que a unidade é dividida em partes iguais.
Mais exemplos de leitura dos números fracionários por extenso:
- 5/10 = cinco décimos (ou dez avos);
- 30/60 = trinta sexagésimos (ou sessenta avos);
- 25/100 = vinte e cinco centésimos (ou cem avos);
- 25/1.000 = vinte e cinco milésimos (ou mil avos).
Lista de números fracionários
A seguir, delimitamos uma lista com os principais números fracionários, bem como sua leitura correspondente:
- 2 – meio ou metade;
- 3 – terço;
- 4 – quarto;
- 5 – quinto;
- 6 – sexto;
- 7 – sétimo;
- 8 – oitavo;
- 9 – nono;
- 10 – décimo;
- 11 – undécimo ou onze avos;
- 12 – duodécimo ou doze avos;
- 13 – treze avos;
- 14 – catorze avos;
- 15 – quinze avos;
- 16 – dezesseis avos;
- 17 – dezessete avos;
- 18 – dezoito avos;
- 19 – dezenove avos;
- 20 – vigésimo ou vinte avos;
- 21 – vinte e um avos;
- 30 – trigésimo ou trinta avos;
- 40 – quadragésimo ou quarenta avos;
- 50 – quinquagésimo ou cinquenta avos;
- 60 – sexagésimo ou sessenta avos;
- 70 – septuagésimo ou setenta avos;
- 80 – octogésimo ou oitenta avos;
- 90 – nonagésimo ou noventa avos;
- 100 – centésimo;
- 101 – cento e um avos;
- 200 – ducentésimo ou duzentos avos;
- 300 – trecentésimo ou trezentos avos;
- 400 – quadringentésimo ou quatrocentos avos;
- 500 – quingentésimo ou quinhentos avos;
- 600 – sexcentésimo ou seiscentésimo ou seiscentos avos;
- 700 – septingentésimo ou setecentos avos;
- 800 – octingentésimo ou oitocentos avos;
- 900 – nongentésimo ou novecentos avos;
- 1000 – milésimo ou mil avos;
- 1001 – mil e um avos;
- 10 000 – décimo milésimo ou dez mil avos;
- 100 000 – centésimo milésimo ou cem mil avos;
- 1 000 000 – milionésimo;
- 1 000 000 000 – bilionésimo;
- 1 000 000 000 000 – trilionésimo.
Tipos de frações
A seguir, podemos conferir os principais tipos de frações e suas definições.
- Frações Próprias: são as frações em que o numerador é diferente de zero e menor que o denominador, ou seja, representam um número menor que um inteiro. Por exemplo:
1/7
- Frações Impróprias: são as frações em que o numerador é maior que o denominador e sempre representam um número maior que um inteiro. Por exemplo:
37/6
- Frações Mistas: são as frações constituídas por uma parte inteira e uma parte fracionária. Também é uma segunda maneira de representar as frações impróprias. Por exemplo:
91/10
Para transformar uma fração imprópria em fração mista é necessário dividir o numerador da fração pelo seu denominador.
- Frações Equivalentes: são as frações que mantêm a mesma proporção de outra fração. Também são chamadas de frações correspondentes.
Para estabelecer frações equivalentes, basta multiplicar os numeradores e denominadores por algum número natural diferente de zero. Por exemplo:
a) Frações equivalentes de:
1/5
1/5 = 2/10 = 4/20 = 8/40 = 16/80
- Frações Aparentes: são aquelas em que o numerador é múltiplo do denominador. Desse modo, elas apenas têm a “aparência” de uma fração, e por isso, recebem esse nome. Por exemplo:
50/2
- Frações Irredutíveis: são as frações que não podem ser simplificadas. Para alcançar uma fração irredutível é necessário dividir ambos os termos pelo máximo de divisores comuns entre eles. Por exemplo:
8/16
Dividindo o numerador e o quociente por 8 obtemos a fração irredutível de:
1/2
- Frações decimais: são frações em que o denominador é um múltiplo do número 10. Por exemplo:
1/10; 3/100; 5/1000
Toda fração decimal pode ser representada por um número decimal, ou seja, um número que possui uma parte inteira e uma parte decimal, quando o número tem vírgula. No exemplo acima, as frações seriam representadas por 0,1; 0,03 e 0,005, respectivamente.
Ademais, é importante assinalar que todos os números escritos em forma de fração são chamados de Números Racionais.
Operações com números fracionários
Assim como os números naturais, os números fracionários também podem ser aplicados nas operações matemáticas de adição, subtração, multiplicação e divisão. Confira:
Adição
Na adição de frações consideramos primeiro o quociente. Se eles forem iguais, basta somar todos os numeradores, mantendo o mesmo denominador. Exemplo:
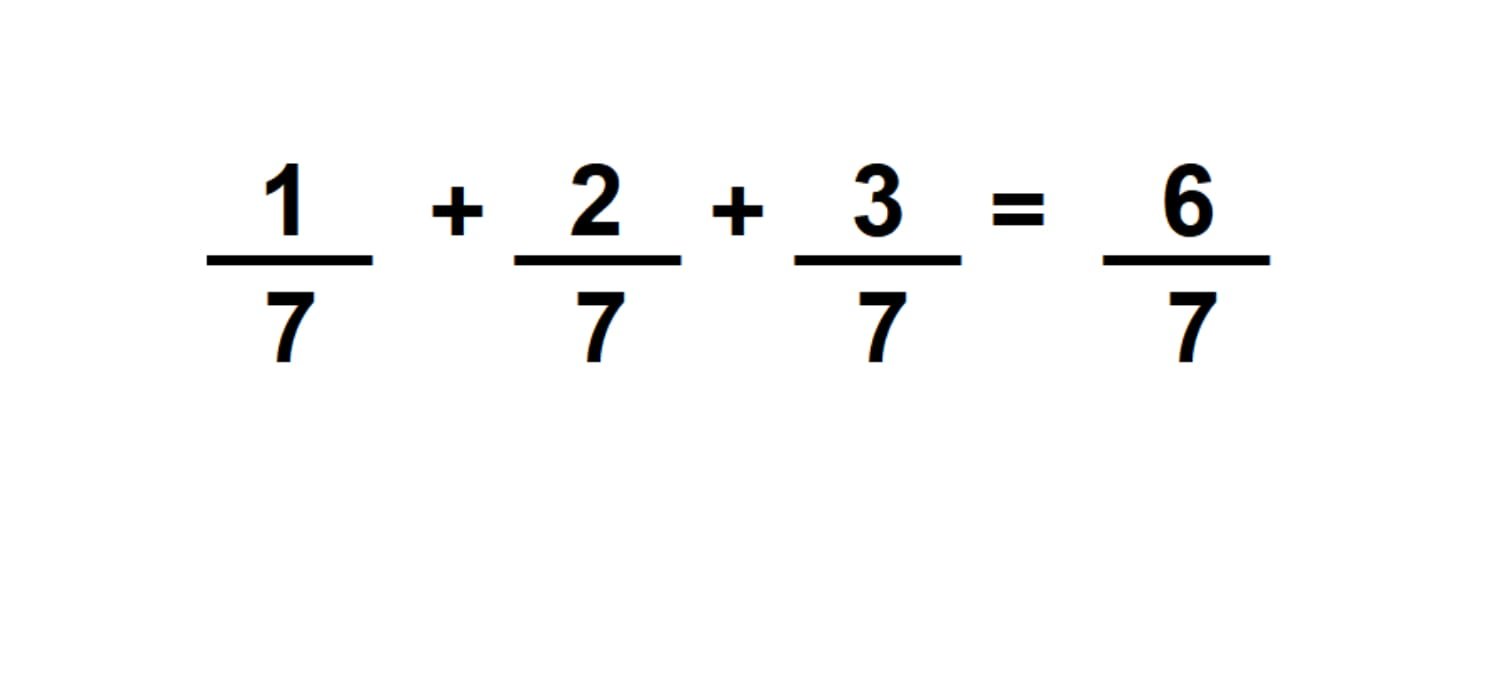
Para os denominadores diferentes, entretanto, é necessário realizar cálculos para converter as frações e obter denominadores de valores iguais.
Para isso, escolhemos como denominador o resultado do mínimo múltiplo comum (MMMC). Assim:
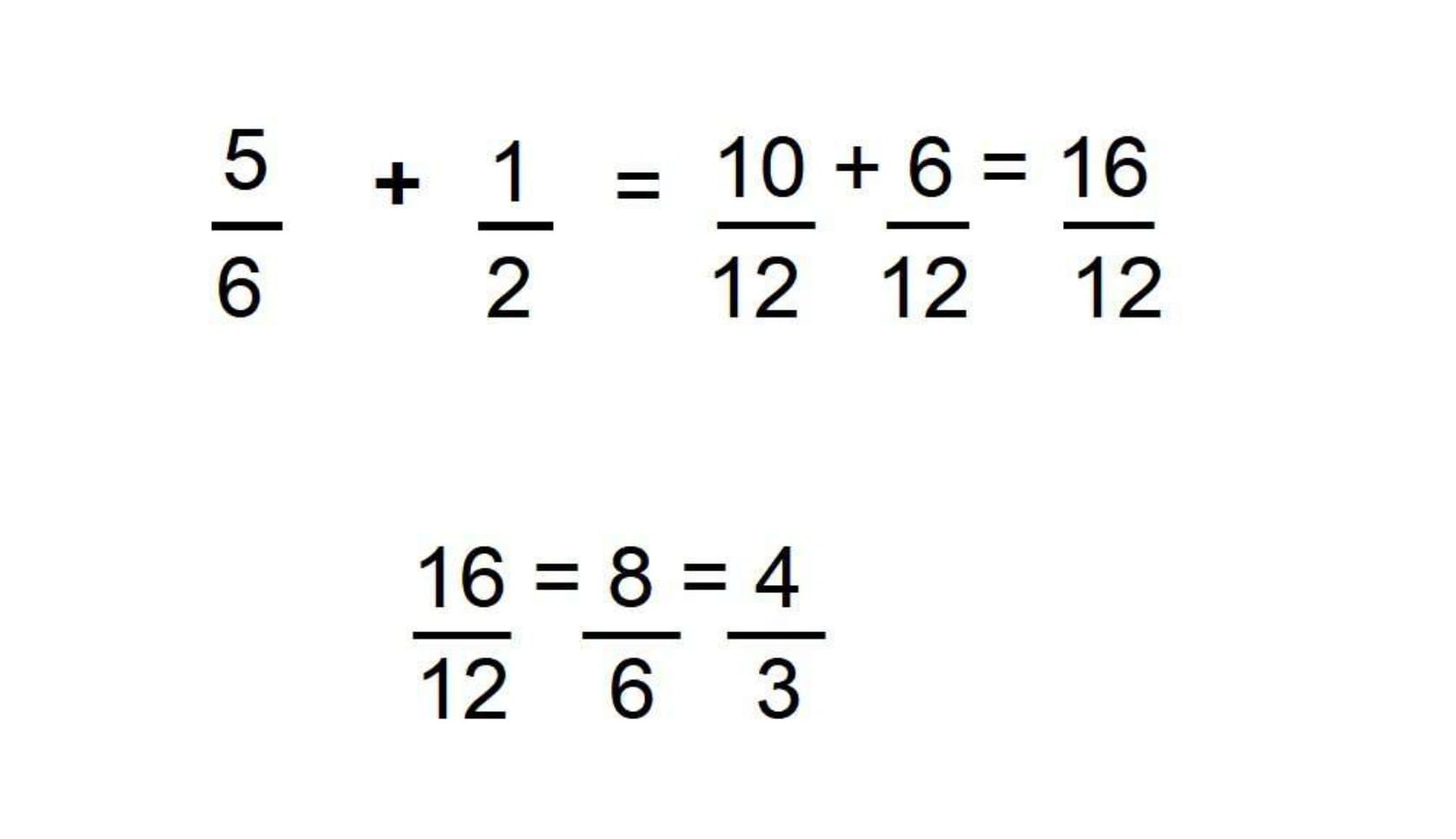
Subtração
Na subtração de frações ou diferença de frações, vale a regra para o mesmo denominador, bastando apenas subtrair os numeradores e manter o denominador em comum. Exemplo:
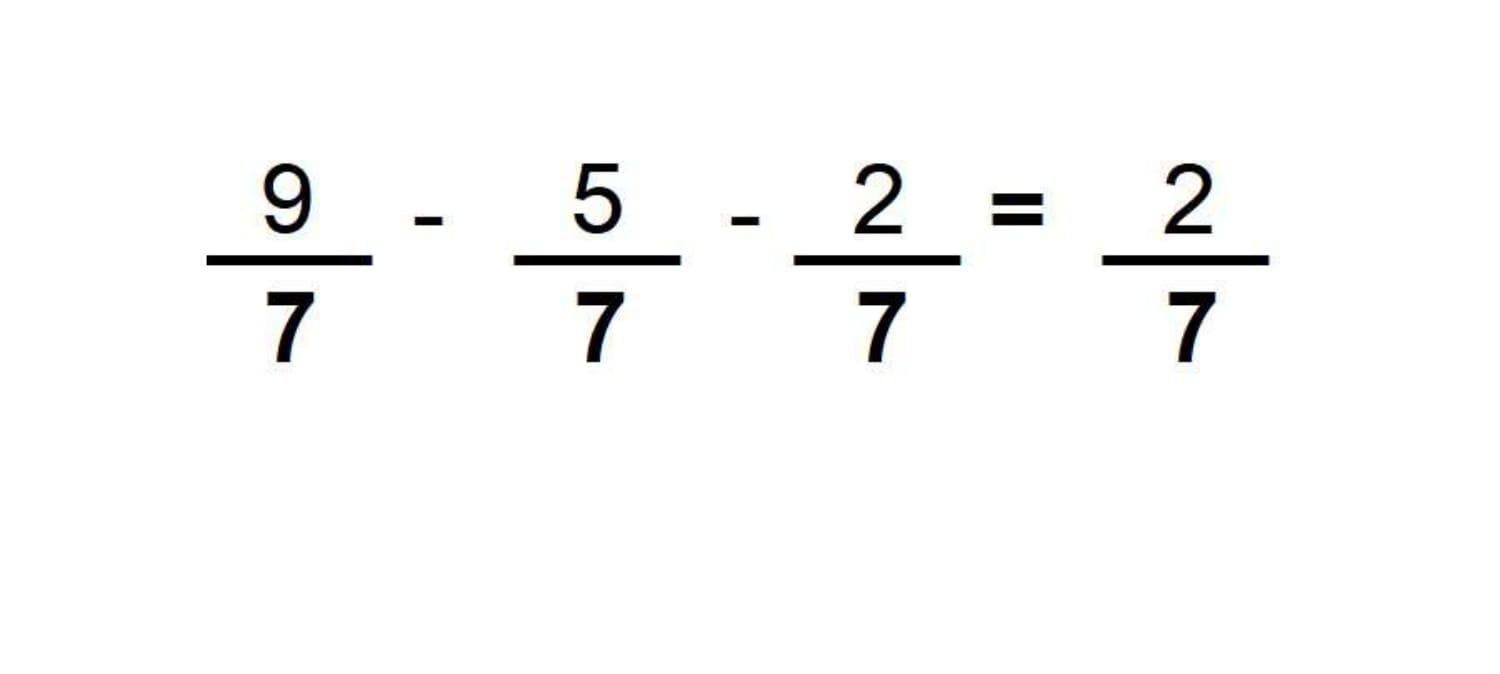
Da mesma maneira, nas frações de subtração com denominadores diferentes é necessário calcular o MMC para encontrar um denominador de valor igual. Assim:
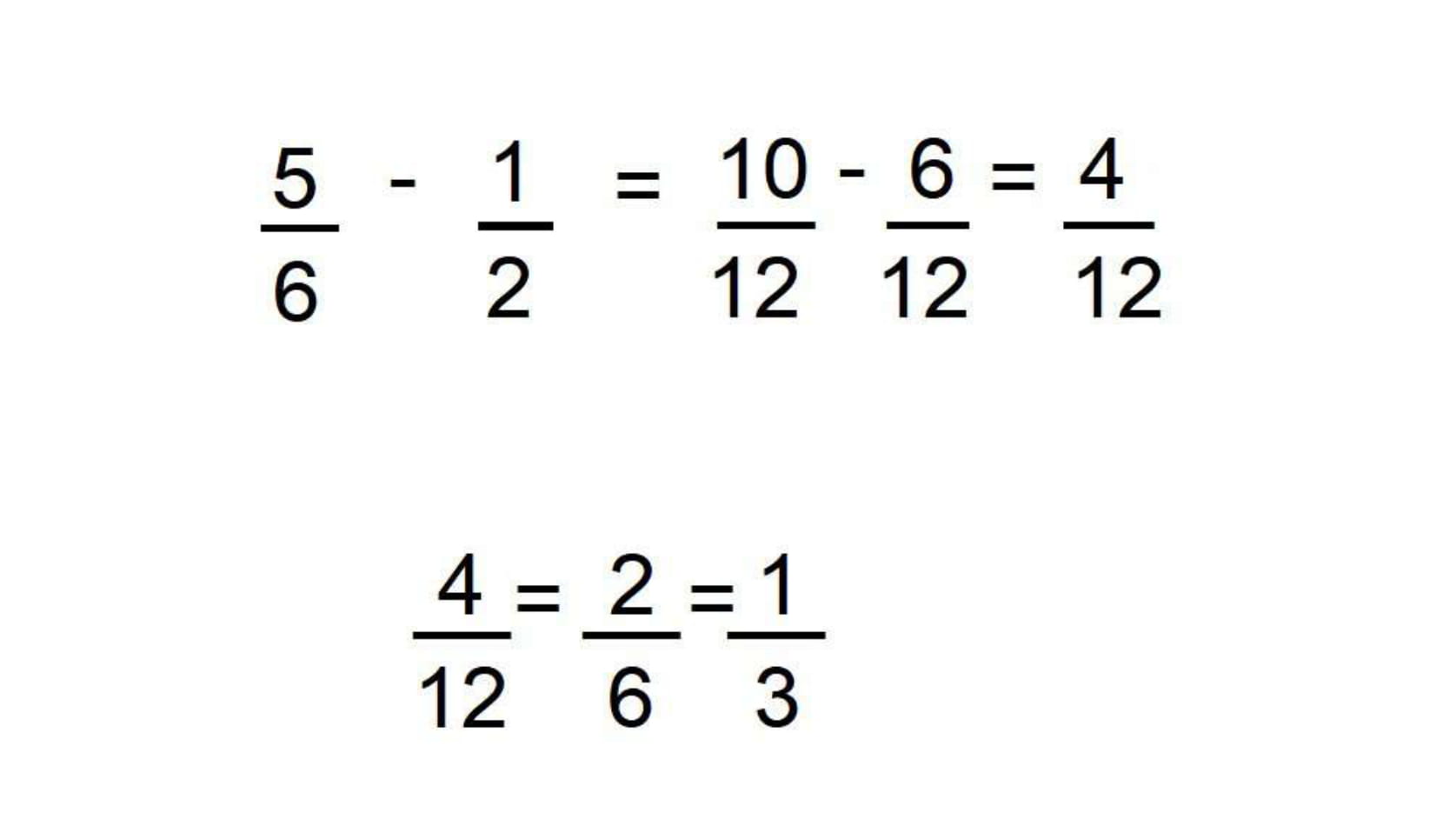
Multiplicação
A multiplicação de frações, por sua vez, é realizada multiplicando o numerador da primeira fração com o numerador da segunda fração. Em seguida, multiplica-se o denominador da primeira com o denominador da segunda. Por exemplo:
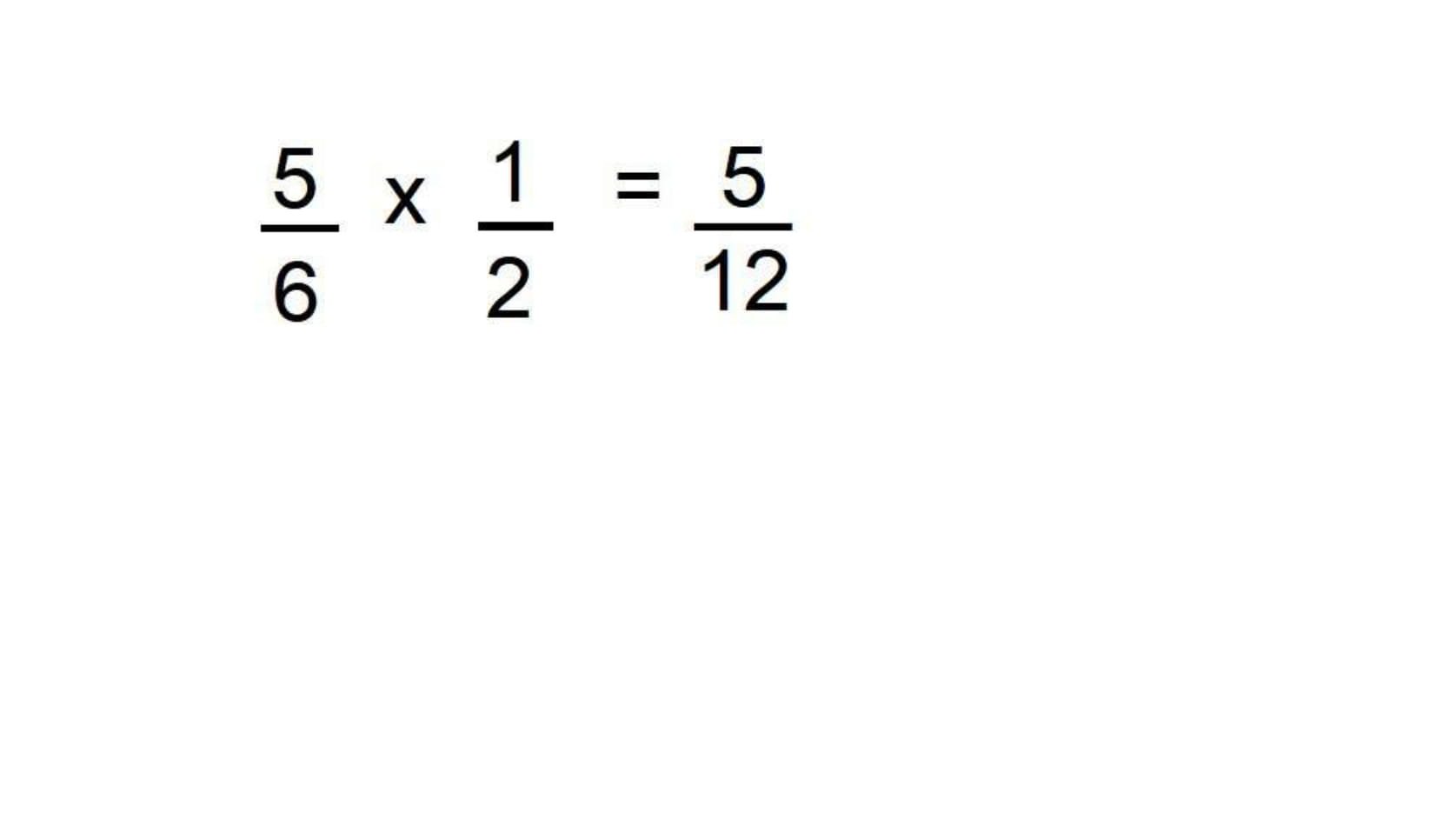
Se a operação envolver mais de duas frações a operação é efetuada da mesma maneira, sucessivamente.
Divisão
Por fim, para a divisão dos números fracionários é preciso multiplicar a fração pela inversão da segunda fração, ou seja, basta manter a primeira e multiplicá-la pelo inverso da segunda. Por exemplo:
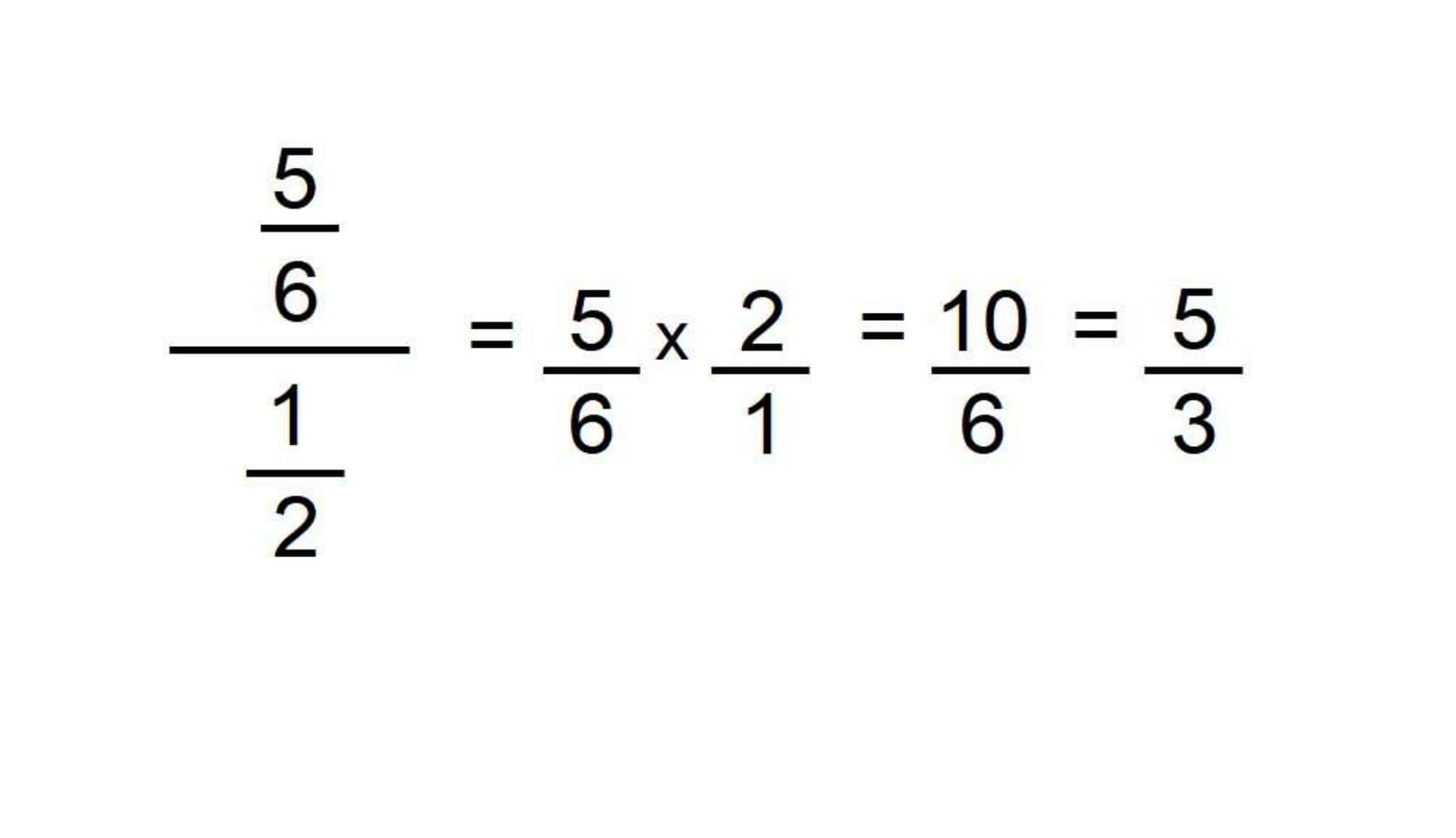
Teste Final
A seguir, você confere um exercício de matemática aplicado em um concurso público renomado para testar seus estudos dos números naturais e números fracionários:
1) Felipe comprou alguns pares de meias e gastou um total de R$ 90,00. Alguns pares custaram R$ 12, 00 cada um e os outros custaram R$ 15,00 cada um. Sabendo que Felipe comprou pelo menos um par de R$ 15,00 o número máximo de pares de meia de R$ 12,00 que Felipe comprou foi:
a) 6
b) 5
c) 4
d) 3
e) 2
Solução: Partimos da primeira hipótese de que Felipe comprou pelo menos um par de meias por R$ 15,00. Como a compra totalizou R$ 90,00 iremos subtrair R$ 15,00 deste total, restando R$ 75 reais.
Partindo do princípio que 75 não é múltiplo de 12, sabemos que Felipe não irá comprar pares de meia por R$ 12 reais. O que elimina a possibilidade da compra de um par de meias por R$ 15,00.
Vamos para a segunda hipótese: Supondo que Felipe comprou 2 pares de meia por R$ 15 reais, totalizando R$ 30,00. Ora, se o total é R$ 90 reais e Felipe gastou R$ 30,00 então estariam faltando 60 reais.
Sendo 60 múltiplo de 12 podemos realizar a divisão, obtendo o resultado de 5 pares de meia. Conclusão: A resposta correta é a letra b, cinco pares de meias.








